
Colligative properties (A-level physical chemistry)

Colligative properties
These are behaviors of solution which depend on the number of nonvolatile dissolved particles (Ions, molecules, atoms, etc.) other than the chemical nature of the solute.
They include:
- Freezing point depression
- elevation of boiling points
- lowering of the vapor pressure
- osmotic pressure
Application of Colligative properties
These properties are used in the determinations of molecular masses of substance.
Trial 1
- Explain the term Colligative property.
- State four Colligative properties of solution.
1. Depression of freezing point
When a nonvolatile solute dissolves in a solvent, the freezing point of the solution is lower than that of the solvent.
The difference between the freezing points of the solvent and solution is called freezing point depression, ∆t.
The depression of freezing point depends on the following rules.
- Depression of freezing point of a given mass of solvent is proportional to mass of a solute dissolved; i.e., the more solute dissolved in a solvent, the lower the freezing point of the solution and the bigger the freezing point depression.
- The freezing point depression for a given mass of solvent is inversely proportional to the molecular mass of the solute.
Thus, when the mass (m) of a solute of relative molecular mass (Mr) dissolved in a given amount of solvent cause a freezing point depression (∆t) degrees Celsius

It follows that depression of freezing point is proportional to the number of moles of a solute and if the same number of moles were present for a different solute, in the same mass of solvent, the freezing point depression would be the same.
Cryoscopic constant

Definition
Cryoscopic constant (Kf) is the amount by which the freezing point of 1000g of a solvent is lowered by 1 mole of solute; assuming rules a and b still hold at this concentrations.
The cryoscopic constants for commonly used solvents are
Solvent Kf/0Cmol-1
Water 1.86
Benzene 5.12
Ethanoic Acid 3.5
Camphor 40.0
Note: cryoscopic constants are sometimes given for 100g of solvent. E.g. for 100g of water = 18.60Cmol-1.
Determination of cryoscopic constant
The rationale of the experiment is to determine the freezing point of a dilute solution of a nonvolatile solute and the work out the freezing point depression of a solution containing 1mole of a solute in 1000g of solvent.
The major problem is that the depression of freezing point of a solvent is usually very small thus, a very sensitive thermometer like Beckmann’s thermometer is required.
a. Beckmann’s procedure
- A given mass of the solvent (m1) is placed in glass tube A into which a thermometer is immersed. This tube is fitted with a wire stirrer, s1, and a side arm, m, through which the solute can be introduced.
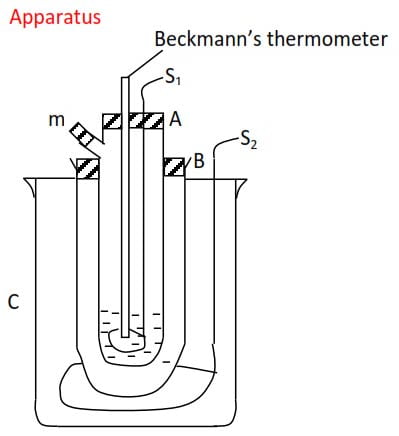
2. The tube A is surrounded by a wider tube, B, which provides an air jacket to ensure uniform cooling
3. The freezing agent is contained in vessel C consisting of a mixture of ice and salt and is kept stirred by stirrer S2.
4. The freezing point of the pure solvent T1, is determined by stirring both freezing agent and the solvent and recording the constant temperature at which a liquid turns into a solid.
5. After determining the freezing point of a solvent the solid is warmed to melt.
6.A given mass of solute m2 is introduced into the solvent through side arm, m, and stirred until completely dissolved.
7. Repeat procedure 4 and note the temperature (T2) at which pure solvent alone separate out from solution as solid.
Treatment of results
Mass of solvent = M1
Mass of solute = m2
∆t = (T1-T2)
Molecular mass of solute = Mr
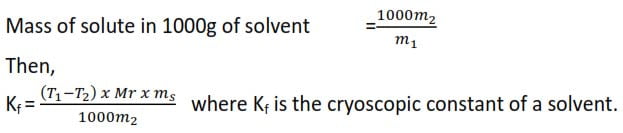
b. Rast’s method
This is based on the use of melted camphor as a solvent because it has un usually high cryoscopic constant. An ordinary (360 degree) thermometer is used instead of Beckmann’s thermometer.
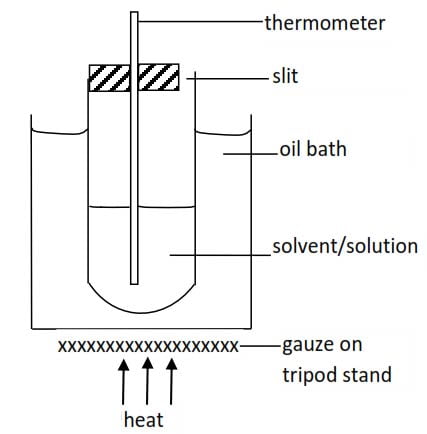
The procedure consists essentially of measuring the melting point of pure camphor and that of the mixture as described in Beckmann’s procedure.
Limitation of the cryoscopic method
A correct value for relative molecular mass (that is a value corresponding to the actual molecular formula) is obtained under the following conditions.
- When the solution freezes, the pure solvent alone must separate out.
- There must be no chemical reaction between solute and solvent. For example, the formula mass of phosphorous pentachloride cannot be determined using this method in water because the two react.
- The dissolved substance must not dissociate or associate appreciably. Thus this method is not suitable for strong electrolytes, acids and bases.
When the solute dissociates the number particles in solution increase causing the apparent molecular mass of the solute to decrease.
When the solute associate the number of solute molecules in solution decrease, the apparent molecular mass will be greater than the actual value
For example, the apparent relative molecular mass of ethanoic acid in benzene is double because two molecules of ethanoic Acid associate to give one molecules.
4. The solution must be dilute.
5. The freezing point method is not suitable for determining the molecular mass of polymers because the freezing point depression for dilute solution of the polymers is negligible.
Example 1
0.55g of nitrobenzene in 22g of ethanoic acid depresses the freezing point of the latter by 0.780C. Calculate the relative molecular mass of nitrobenzene. [The cryoscopic constant for 1000g of ethanoic acid is 3.900Cmol-1]

Example 2
0.72g of a compound X was dissolved in 80g of water and the resultant solution had a freezing point of -0.140C. When 2.9g of the same compound was dissolved in 11g of benzene, the depression was 60C. [Kf for water is 1.86 0Cmol-1kg-1 and Kf for benzene is 5.50Cmol-1kg-1.)
(a) Calculate the apparent molecular mass of X in
(i) water
(ii) Benzene
(b) comment on the results


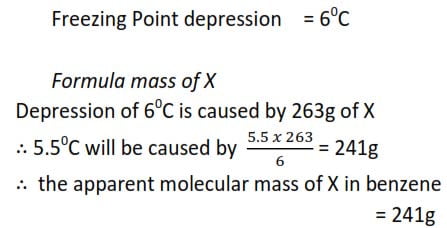
(b) The apparent molecular mass is X is in benzene is double that in water probably because two molecules of X associate in benzene to give one molecule. Or one molecule of X dissociates into two particles in water.
(b) Elevation of Boiling point
When a substance a nonvolatile solute is dissolved in a solvent, the boiling point of the solution is higher than the boiling point of the solvent.
The difference in boiling point of the solution and solvent is called boiling point elevation, ∆t .
(i) Elevation of boiling point of a given mass of solvent is proportional to mass of a solute dissolved.
(ii) Elevation of boiling point for a given mass of solvent is inversely proportional to the molecular mass of the solute.
Thus, is the mass (m) of a solute of relative molecular mass (Mr) dissolved in a given amount of solvent cause a freezing point depression (∆t) degrees Celsius

It follows that elevation of boiling point is proportional to the number of moles of a solute and if the same number of moles were present for a different solute, in the same mass of solvent, the Elevation of boiling point would be the same.
Ebullioscopic/boiling point constant Kb

The constant of proportionality Kb is called the boiling point constant of the solvent.
Definition
Boiling point constant (Kb) is the amount by which the boiling point of 1000g of a solvent is raised by 1 mole of solute; assuming rules (a) and (b) still hold at this concentration.
The boiling point constants for commonly used solvents are
Solvent Kf/0Cmol-1
Water 0.51
Benzene 2.67
Ethanoic Acid 3.08
Limitation of this method in determination of the relative molecular masses of substance
- Solution must be dilute
- Solute should not react with solvent
- Solute must not associate or dissociate in solution
- Substance must be stable at boiling point of the solution and non-volatile
- It is not suitable for determination of molecular masses of polymers because dilute solutions of polymers, produce negligible boiling point elevation.
Method for determining the boiling point elevation
The main difficult for finding molecular masses by this method arises from super heating of the liquid above its true boiling point. This can be minimized by the following methods.
- Cottrell’s method

- The solvent is heated in a wide tube, A, fitted with a side arm leading to a reflux condenser which condenses the vapor of the boiling solvent and returns it to the boiling tube.
- A is closed by a stopper, through which passed a second tube B, open at the lower end. B contains a Beckmann thermometer.
- The bulb of the thermometer is above the liquid and protected by the inner tube from drops of condensed liquid falling to it from the side arm.
- Partially immersed in liquid is the Cottrell’s ‘pump’, C, consisting of small inverted glass funnels with a step which divides into two narrow tubes. These are bending around at the top so that, when the liquid boils, the vapor forces the liquid to rise up the narrow tube and spray the bulb of the thermometer. This prevents super heating, and as further precaution is a platinum wire sealed through the bottom of the tube A at D. Heating is by micro burner, which is shielded from draught.
- First, we read the Beckmann thermometer for boiling point (T0) a known mass (ms g) of solvent. Then we introduce a weighed solute (mass M2 g) through the side arm and determine the boiling point (T1) of the solution.
This method can be used to determine the molecular mass of benzoic acid dissolved in acetone or that of naphthalene dissolved in chloroform.
Treatment of results
Mass of solvent = ms
Mass of solute = m2
∆t = (T1-T0)
Molecular mass of solute = Mr
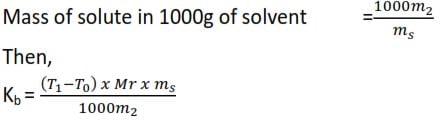
where Kb is the boiling point constant of a solvent.
Lands Berger’s method
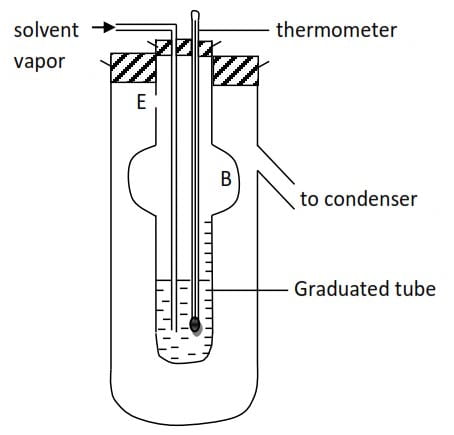
- The solvent is boiled in a separate flask. The vapor passes into the solution which is contained in a graduated tube; surrounded by a second tube.
- The solution is raised to its boiling point by the latent heat of condensation of the solvent vapor.
- When the solution boils the solvent vapor passes through the solution without condensing. It passes through a hole, E, in the boiling tube so that the latter becomes jacketed with the vapor of boiling solvent. Thus reducing radiation to the minimum.
- The bulb B on the inner tube prevent a liquid from being splashed through E.
- The boiling point (T00C) of pure solvent is first found and then a known mass of a solute (m2g and formula mass Mr) is introduced and the boiling point (T10C) of solution is found.
- The final volume of the liquid in the graduated tube is read of and from the density of the solvent the mass (msg) of the solvent into which a solute is dissolved is calculated.
Then the boiling point constant Kb is given by
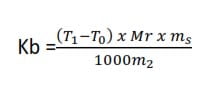
NB. The reason why steam at 1000C raises the temperature of the solution above 1000C is that steam at 1000C has a higher vapor than a solution at the same temperature, it forms a layer above the solution condensing at the surface of the solution and the latent heat evolved would increase the temperature of the solution. The same situation exists when steam is bubbled through the solution.
Example 3
The boiling of ethanol is 780C. Calculate the boiling point of the solution containing 2.7g of ethanamide (CH3CONH2) in 75g of ethanol. (Boiling point elevation constant for 1000g of ethanol = 1.150Cmol-1kg-1)
Solution

(c) Lowering of vapor pressure
The vapor pressure of a liquid at a given temperature is the pressure exerted by it vapor when it is in equilibrium with the liquid.
The vapor pressure of a solution of a nonvolatile solute is usually less than that of pure solvent at a given temperature; because the nonvolatile solute particles occupy part of the solvent surface reducing the escaping tendency of the solvent molecules into the vapor.
Laws of vapor pressure of solution
As with freezing point depression and boiling point elevation; lowering of the vapor pressure of a solvent by a nonvolatile solute at a given temperature is directly proportional to the concentration of the solute and inversely proportional to the formula mass (RFM).

The relative lowering of vapor pressure is
- independent of temperature
- proportional to the concentration of solute
- Constant if the number of molecules of different solute is dissolved in the same mass of solvent.
Raoult’s vapor pressure law
The relative lowering of vapor pressure is equal to the mole fraction of the solute. If n1 and n2 are the number of moles of solute and solvent

When, m1 is the mass of the solute in the solvent of mass m2, and Mr1 and Mr2 are the relative molecular massed of the solute and solvent respectively
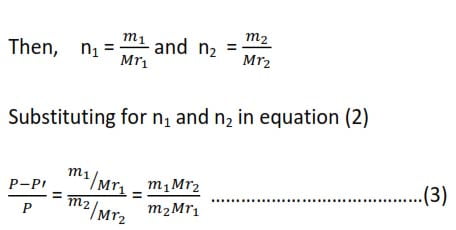
The vapor pressure law (3) holds true if only
(i) the solute is non volatile,
(ii) the solution is dilute;
(iii) the solute does not dissociate or associate appreciably.
Example 4
The vapor pressure of water at 500C is 12333Pa. At this temperature, a solution of 9.14g of carbamide (urea) in 150.0g of water has a vapor pressure of 12106Pa. Find the relative molecular formula of the carbamide.
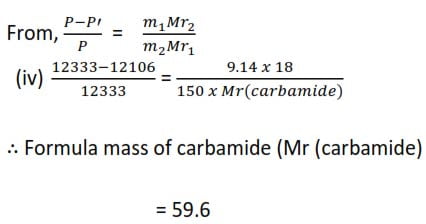
(d) Osmotic pressure method for determining the relative molecular masses of substance.
Definitions
Osmosis is the movement of the solvent molecules from the region where they are highly concentrated to the region of their low concentration through a semi-permeable membrane.
Suppose the solution and solvent are contained in the limbs of a U-tube and a semi-permeable membrane separates a solution from a solvent and that a movable piston is placed on a limb containing the solution. The piston would be observed to rise as the solvent passes through the membrane to the solution. The rise may be prevented by applying just the right external pressure to the piston.
The osmotic pressure of the solution is the minimum pressure which must be applied to the solution to balance the tendency of the solvent to flow from the solvent to the solution side of the semi-permeable membrane.
Laws of osmotic pressure
The Dutch scientist Vant Hoff found out that there is a close resemblance between the osmotic pressure and the gas law
PV = nRT
Since the law analogous to Charles and Boyles law apply to osmotic pressure and an expression similar to gas equation πV = nR’T can be deduced for a dilute solution. Where = osmotic pressure, V= volume of the solution, R’= constant which is very close to the gas constant and T is temperature of the solution in Kelvin.
Calculations on the osmotic pressure method are chiefly used to find RFM of polymers that have high molecular mass.
Example 5
An aqueous solution of sucrose containing 19.15g of sugar per dm-3 has osmotic pressure of 136,300Pa. Find the Relative Formula mass of sucrose.
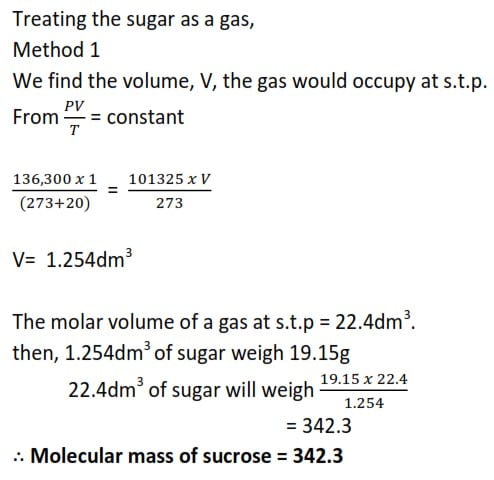
Method II
From πV = nR’T , we find the moles of sugar solution in 19.15g,
NB: Pressure must be in Pascal, Volume in m3, and temperature in Kelvin
π = 136,300Pa
V= 1dm3 = 1×10-3m3
R = 8.31
T = (273+ 20)K = 293K
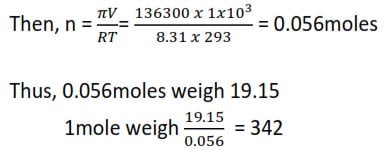
Method III
From πV = nR’T , we find the moles of sugar solution in 19.15g,
NB: Pressure must be in atmospher, Volume in dm3, and temperature in Kelvin, R= 0821
π = 136,300Pa = 136300/101325 = 1.345atm
V= 1dm3
R = 0.0821
T = (273+ 20)K = 293K

NB. The only problem with the second method is that, there is a need to convert units to standard units of Pressure (Nm-2/ Pascal), Volume, (m3), and temperature (Kelvin)
Precautions to osmotic law
- the solution must be dilute
- the solute should not dissociate or associate in solution
- the solute should not react with the solvent
- the temperature should not be very high of very low.
Method of determination of Relative formula mass of a substance by osmotic pressure method
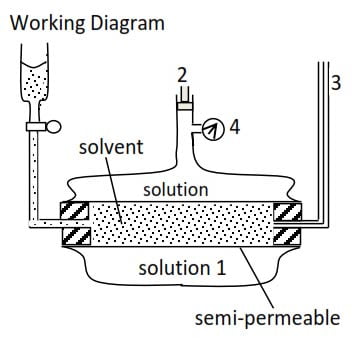
- cylindrical tube between the solvent and solution is porous/semi-permeable
- Pressure is applied to the solution and adjusted until there no flow of solvent into solution.
- Capillary tube indicates movement of solvent into the solution.
- Osmotic pressure, P (Pascal) obtained from the pressure gauge and temperature T0C of the solution is determined
Results

Watch this
Sponsored by The Science Foundation College +256 753 80 27 09
Compiled by Dr. Bbosa Science

Thank u very much sir but this page has issues with downloading the work the first time it worked wonders but now all we get is error 404
we are going to work on it
I really like forgathering utile info, this post has got me even more info! .
there are bargain dvd players that are sold in our area. i think they are generic low cost dvd players,.
A very very interesting article! I’ll try to track that continues here! Thank you.
I couldn’t resist commenting. Perfectly written! https://zeleniymis.com.ua/
A great post without any doubt.
Thanks for shedding light on this. Electronics