
Gas laws (A-level physical chemistry)

Physical behavior of gases
Kinetic theory
This is useful in accounting for the known properties of gases, liquids and solids. The ideas underlying the kinetic theory, may be summarized as follows:
(i) Matter is made up of atoms/small particles/molecules
(ii) The particles in a gas are in continuous rapid random motion in straight line in every direction and them colliding with each other and with the walls of the container. The pressure exerted by the gas on the container wall is due to bombardment by moving particles.
(iii) The particles in a gas are separated from each other by distances which are large compared to the size of the particles (particles in a gas are very far apart and they are very small)
(iv) Collision of gas particles are regarded as being perfectly elastic (such that there is no loss in kinetic energy)
Gas laws
The following laws were formulated from results of the experimental observation in the behavior of gases.
Gay Lussac’s law of combining volumes
States that “when gases combine together at a given temperature and pressure, the do so in volumes which bear a simple ratio to each other and to the volume of the product if it is a gas
Example 1
40 cm3 of oxygen was added to 30 cm3 of carbon monoxide and the mixture ignited. What is the volume and composition of the resulting mixture? (All volumes measured at the same temperature and pressure).
2CO (g) + O2 (g) → 2CO2 (g)
2 mole 1 mole 2 moles
2 vol. 1 vol. 2 vol. (Gay-Lussac’s Law)
30 cm3 15 cm3 30 cm3 (volume ratio)
The volume of CO2 produced is the same as that of CO used up, i.e. 30 cm3 of CO2 are produced.
15 cm3 of the 40 cm3 of oxygen are used up in the reaction, i.e. 25 cm3 of oxygen remain un reacted
30 cm3 of carbon dioxide produced and 25cm3 of un reacted oxygen give total volume is 55 cm3.
Trial 1
10 cm3 of a gaseous hydrocarbon were mixed with 90 cm3 of oxygen and sparked. The resulting volume at r.t.p. was 70 cm3, which reduced to 30 cm3 on shaking with sodium hydroxide. Find the empirical formula of the hydrocarbon.
The physical behavior of gases is described by four gas laws which include
- Boyles’ law
- Charles law
- Daltons law of partial pressures
- Graham’s law of diffusion
Boyles’ law
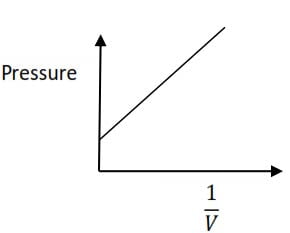
It state that the volume of a given mass of a gas is inversely proportional to its pressure at constant temperature
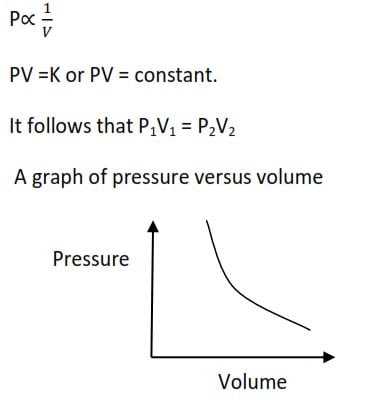
A graph of pressure against the inverse of volume gives a straight line
Charles’ Law
It states that the volume of a given mass of a gas is directly proportion to its temperature at constant pressure.
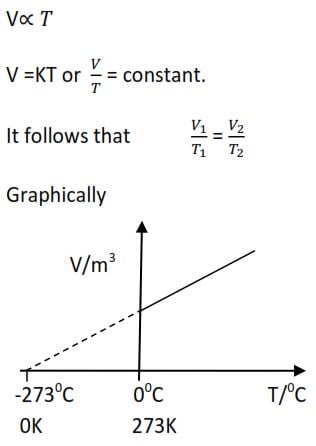
NB: The units of temperature in all gas laws are Kelvin. However, units of pressure and volume vary, although must be the same in a given situation.
Pressure law
It is a modified version of Charles law. it states that pressure of a given mass of a gas is directly proportional to its temperature at constant volume.
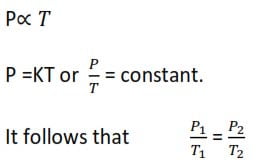
The Ideal gas equation
Boyle’s law and Charles’ laws can be combined to give a single equation which represents the relationship between, volume, pressure and temperature of a given mass of a gas.
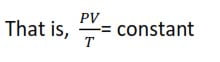
When the quantity of the gas is 1 mole, the constant K is referred to as a molar gas constant, represented as R
For 1 mole of a gas PV = RT
For n moles of a gas
PV = nRT (the ideal gas equation)
Conditions at “standard temperature and pressure (s.t.p)
Temperature = 273K or 00C
Pressure = 760mmHg or 1 atmosphere or 101325 Pascal
Molar volume of a gas (volume occupied by 1 mole of a gas) = 22.4dm3 or 22400cm3
Conditions at “room temperature and pressure (r.t.p)
Temperature = 278K or 250C
Pressure = 760mmHg or 1 atmosphere or 101325 atmospheres
Molar volume of a gas (volume occupied by 1 mole of a gas) = 24dm3 or 24000cm3
NB. When using ideal gas equation PV =nRT, pressure, and volume must be changed to Pascal and m3 while the unit of temperature must be in Kelvin.
Example 2
A certain mass of a gas occupies a volume of 24dm3 at 180C and a pressure of 100.4kPa. Calculate the volume of a gas at s.t.p.

Example 3
1.18g of a compound on vaporization occupied 300cm3 at s.t.p.
(a) Calculate the relative molecular mass of P.
300cm3 weigh 1.18g
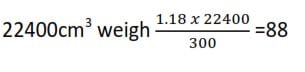
Trial 2
0.13g of P occupies 112 cm3 at s.t.p
Calculate the formula mass of P
Trial 3
When 0.225g of T was vaporized at 1270C and 760mmHg, it occupied 119.11cm3. (Molar volume at s.t.p is 22.4dm3).
Calculate the molecular mass of T
Trial 4
When vaporized 0.1g of a compound A occupied 54.5cm3 at 2080C and 98.3kPa; determine the molecular formula of A
Deviation from Ideality
Ideal gases are those that obey ideal gas equation. These gases are not common and most gases tend to deviate from ideality. A gas is said to be ideal (perfect) if
(i) occupies a negligible volume compare to volume of container
(ii) when there is no forces of attraction between its molecules.
(iii) collision of particles is perfectly elastic
Real gases
These do not obey the ideal gas law exactly because at high pressure and low temperature the volume occupied by gas molecules and the forces of attraction between the molecules is not negligible.

NB. The higher the intermolecular forces, the higher the deviation, e.g. in NH3.
Correction of volume and Pressure for the real gas to account for intermolecular forces and volume
To account for molecular volume and intermolecular forces J.H. Vander Waal proposed that
(i) The volume of gas molecules reduces the actual volume of the container the molecules are left to move i.e. the volume of the container is not the volume in which molecules can move. The actual volume open to them is less than that of the container. For this reason Van der Waal wrote the volume of the gas as (V-nb) where n is the number of moles of a gas and b is the volume that is no longer available to each mole.

A plot of a graph of pressure versus volume at different temperatures give lines called isotherms shown below.
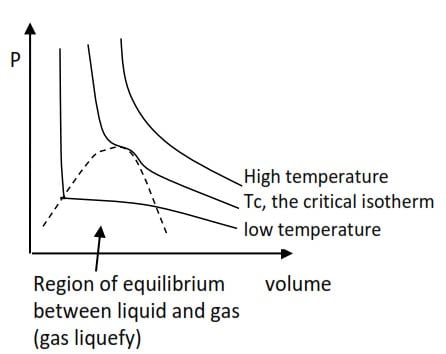
NB. The critical isotherm marks the border between gases and liquids. The temperature of critical isotherm is called critical temperature, Tc. Above; Tc a gas will not liquefied no matter how high the pressure. Each gas has its own critical temperature because the strength of the intermolecular forces in each gas are different. Below the critical temperature a gas will be liquefied when the pressure is high enough.
Trial 5
The curves below show a plot of pressure against molar volume at different temperatures of carbon dioxide
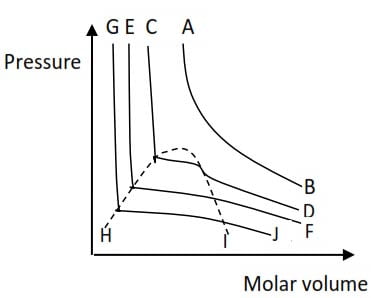
(a) State the curve which represent the highest temperature (1 mark)
(b) What do the following lines represent
(i) HI (ii) GH
(c)(i) Explain what is meant by the term critical temperature
(c) (i) Draw a sketch on the graph a line that represent isotherm of critical temperature.
Trial 6
(a) The diagram in figure 1 shows isotherms of a gas.

(i) What is the critical temperature
(ii) Which isotherm almost represent the behavior of an Ideal gas
(iii) What does the region ABC represent
(b) State one condition necessary for liquefying a gas.
Graham’s Law of gaseous diffusion and effusion
Graham’s Law of diffusion of gases state that “the relative rates of diffusion of gases, under the same conditions, are inversely proportional to the square roots of their densities.”
Diffusion is the movement of gas particles from a region of high concentration to a region of low concentration
Comparing the rate of diffusion of gases A and B
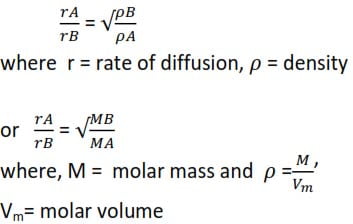
Graham’ Law also applies to gaseous effusion. Effusion is the passage of a gas through a very small hole into a vacuum.
Example 4
50cm3 of a gas A effuse through a tiny aperture in 146s and the same volume of carbon dioxide effuse under the same condition in 115s. Calculate the molar mass of A.

(ii) A gaseous Alkane diffuses through a porous partition at a rate of 2.56cm3s-1. Helium diffuses through the same partition under the same conditions at a rate of 8.49cm3s-1. What is the molar mass of Alkane? What is the its molecular formula a

Trial 7
(i) State Graham’s Law. (2marks)
(ii) Oxygen diffuses through a small hole 0.935 times faster than gas X. Calculate the relative molecular mass of X (4marks)
Trial 8
(a) A gaseous compound contains 44.4% carbon, 51.9% nitrogen, and hydrogen. Determine empirical formula of X.
(b) 50ml of X diffuses through a porous plugin 25 second. Under similar conditions, the same volume of hydrogen gas diffuses in 6.8 seconds. Calculate
(i) the molecular mass of X
(ii) The molecular formula of X
Dalton’s Law of Partial Pressure
The total pressure exerted by a mixture of gases that do not react chemically is the sum of the pressure that the individual gases would exert if they were to occupy the same volume alone.
In symbols, for a mixture of gases A and B, the total pressure (Pt) is given by
Pt = PA + PB
The mole fraction of a gas A, in the mixture, is given by
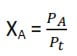
Example 5
4.0dm3 of oxygen at a pressure of 400kPa and 1dm3 of nitrogen at 200kP were introduced into a 2.00dm3 vessel. What is the total pressure in the vessel?
Solution
When oxygen contracts from 4.00dm3 to 2.00dm3 the pressure increases to

The partial pressure of oxygen = 800kPa
When nitrogen expands from 1.0 dm3 to 2.0 dm3, the pressure decreases from 200 kPa to

The partial pressure of nitrogen = 100kPa
Total pressure = P(O2) + P(NH3)
= 800+ 100 = 900kPa
the total pressure = 900kPa.
Trial 9
(a) State what is meant by the term an ideal gas. (01 mark)
(b) Explain how liquefaction of a gas can be affected by
(i) Pressure (2 ½ marks)
(i) Temperature (2 ½ marks)
The curve below shows deviation of some gases from ideal behaviors.

(i) State why hydrogen shows a small deviation from ideal behavior compared to other gases (1 ½ marks)
(ii) Compared to deviations of oxygen and carbon dioxide from ideal behavior. (2 ½ marks)
Questions? Download PDF
Gas laws (Boyles, Charles, pressure, Daltons, Grahsms ) laws

i want to knw wat region ABC represents on the graph about liquification a gas
gas liquify inthe the region where the gas and liquid are in equilibrium
Good