Newton’s laws of motion (A-level physics)

Newton’s laws of motion

First Newton’s law of motion.

A body remains in its state of rest or uniform motion in straight line unless an external force acts on it.

This law, also called the principle of inertia. Inertia is reluctance of a body  to start moving once at rest or stop moving once in motion.

Inertia depends on the mass of the body thus the mass is a measure of inertia.

Second Newton’s Law of motion

The rate of change of momentum is directly proportional to the magnitude of of the applied force producing it and takes place in the reaction of the applied force.

Momentum is the product of mass of the body and its velocity.

Third Newton’s law of motion

For every action, there is an equal and opposite reaction.

For example 1

A block of mass 2 kg is pushed along a table with constant velocity by force of 5 N. When the push is increased to 9 N, what is the resultant force and acceleration?

Resultant force F= 9 – 5 = 4N

But

F = ma

4 = 2a

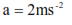
Example 2

Two blocks, A of mass 1kg and B of mass 3kg, are side by side and with contact with each other. They are pushed along the smooth flow under the action of a constant force 50N applied to A. Find

i) The acceleration of the blocks

ii) The force exerted on B by A.

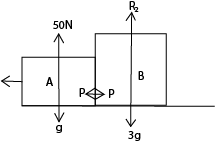
(i) F =ma = 50 = (1+3)a

Acceleration, a = 12.5ms^-2

(ii) Using A

50 – p = 1 x 12.

p = 50 – 12 = 37.5 N

Example 3

A light cord connects 2 objects of masses 10kg and 6kg respectively over a light frictionless pulley. Fins the acceleration and tension in the cord.

Body A

10g –T = 10a …………………………………………….(i)

Body B

T – 6g = 6a  ……………………………………………. (ii)

Eqn (i) – eqn (ii)

4g = 16a

a  = 2.45ms^-2

From equation (ii)

T = 6 x 2.45 + 6 x 9.81 = 73.6N

Example 4

Explain why the tension in a cable of a lift is different when the lift is accelerating upwards from when it it is accelerating downwards.

Solution

When the lift is accelerating upwards, the tension in its cable is equal to weight of the lift and its occupants plus the accelerating force of the lift on its occupants.

When the lift is going down, the lift and its occupants derive their accelerating force from their weight, the tension in the cable is the difference between the weight of the lift and its occupants and accelerating force of the lift and its occupants.

Example 5

(a) Two particles of mass m1 and m2 are connected as shown below by a light inextensible string passing over a smooth fixed pulley. If m1>m2 show that the acceleration of the system is given by

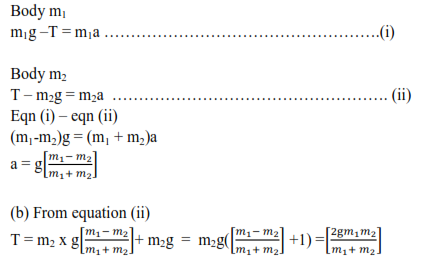
Example 6

A mass m₂ lies on a smooth table connected by a light inextensible string passing over a small smooth pulley at the table to a mass, m₁, hanging freely.

(a) What is the acceleration?

Solution

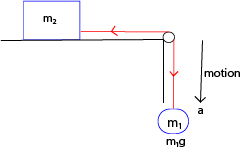
Body m₁

m₁g –T = m₁a …………………………………………….(i)

Body m₂

T – 0 = m₂a  ……………………………………………. (ii)

Substitution Eqn (ii) into  eqn (i)

m₁g-m₂a = m₁a

Example 7

The diagram below shows masses m₁, m₂ and m₃ connected  by light inextensible string such that m₁ and m₃ hang vertically while m₂ lies on horizontal smooth surface with m₁ greater than m₃. Show that the acceleration due to gravity

Motion of a particle on an incline

Let the mass of the particle be m and R be the normal reaction. If the plane makes an angle θ to the horizontal, then the forces which act on the body are shown below;

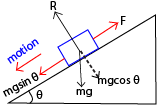
From the diagram

R = mgcosθ

Result force = mgsinθ – F

              ma = mgsinθ – F

if the system is at reest where a = 0

             m(0) = mgsinθ –F

                  F = mgsinθ

For example 8

A body of 3kg slides down a plane which is inclined at 300 to the horizontal. Find the acceleration of the body if

(a) the plane is smooth

(b) there is a frictional resistance of 9N.

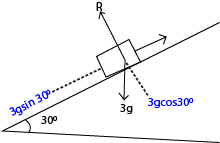
R is the normal reaction

(a) F = ma

     3gsin 30⁰ = 3a

                a = 4.9ms^-2

b) F = 3g sin 300  – 9 = 3a

a = 1.9ms -1

Note friction force acts in the opposite direction of motion.

Example 9

A body of mass 8kg is released from rest on a surface of a plane. If the resisitance to the motion is in acting up the plane and the slope of the plane is 1 in 40. Calculate the acceleration of the body down the plane and the speed acquired in 6 seconds after the release if he resistance to the motion is N

From ma = mgsinθ – friction

Example 10

A block m1 is connected to another m₂ by a light inextensible string which passes over as smooth pulley. If the inclined plane is smooth and m₂>m₁, show that the acceleration of the

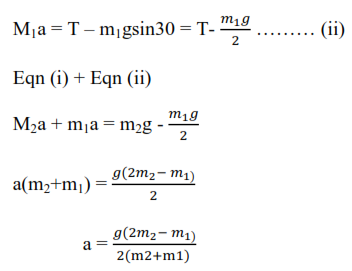
Exercise

1. A body A rests on a smooth horizontal table. Two bodies of mass 2kg and 10kg hanging freely are attached to opposite ends of A by light inextensible strings which pass over smooth pulleys at the edges of the table. The two strings are taut when the system is released from rest; it accelerates at 2ms^-2. Find the mass of A [Answer 27.24kg]

• A rectangular block of mass 10kg is pulled from rest a long a smooth inclined plane by  a light inelastic string which passes over a frictionless pulley and carries  a mass of 20kg as shown below with the plane inclined at angle of 30⁰ to the horizontal.

Sponsored by The Science Foundation College

+ 256 753 80 27 09

Dr. Bbosa Science