
A-level mechanics revision questions fully answered

List of physical constants to be used
Acceleration due to gravity, g 9.81ms-2
Electron charge, e 1.6 x10-19C
Electron mass 9.11 x 10-31kg
Mass of the earth 5.97 x 1024kg
Plank’s constant, h 6.6 x 10-34Js
Stefan’s-Boltzmann’s constant, σ 5.67 x 10-8Wm-2K-1
Radius of the earth 6.4 x 106m
Radius of the sun 7 x 108m
Radius of the earth’s orbit about the sun 1.5 x 1011m
Speed of light in the vacuum, c 3.0 x 108ms-1
Thermal conductivity of copper 390Wm-1K-1
Thermal conductivity of aluminium 210Wm-1K-1
Specific heat capacity of water 4.200Jkg-1K-1
Universal gravitational constant 6.67 x 10-11Nm2Kg-2
Avogadro’s number, NA 6.02 x 1023mol-1
Surface tension of water 7.0 x 10-2Nm-1
Density of water 1000kgm-3
Gas constant, R 8.31Jmol-1K-1
Charge to mass ratio, e/m 1.8 x 1011Ckg-1
Faraday’s constant, F 9.65 x 104Cmol-1
Thermal conductivity of Iron 75Wm-1K-1
Specific latent heat of fusion of Ice 3.3 x 105Jkg-1
Permittivity of free space, μ0 4.0π x 10-7Hm-1
Permittivity of free space, ε0 8.85 x 10-12Fm-1
One electron volt 1.6 x 10-19J
Resistivity of Nichrome wire at 250C 1.2 x 10-6Ωm
Specific heat capacity of copper 400Jkg-1K-1
- (a) (i) Distinguish between scalar and vector quantity. (01 mark)
A scalar quantity is a physical quantity with magnitude but no direction
A vector quantity is a physical quantity with both magnitude and direction
(ii) Give two examples of each type of quantity. (02marks)
Examples of scalar quantities: volume area, distance speed
Examples of vector quantities: force, displacement, impulse, momentum, acceleration
(b) A body of mass 0.2kg at rest is acted on by four forces of 2.8N, 6.0N, 4.5N and 1.2N as shown in the figure below.

Calculate
(i) Resultant force on the body (04marks)

The resultant force is 8.73N in a direction 24.60 below the horizontal axis.
(ii) Distance moved in 4s (02marks)
Using F = ma
8.73 = 0.2a
a = 43.65ms-1
s = ut + ½ at2
= 0 x 4 + ½ x 43.65x 42
= 349.2m
(c) State Newton’s law of motion and use them to derive the law of conservation of momentum. (06marks)
- A body continues in its state of rest or uniform motion in a straight line unless acted upon by an external force
- The rate of change of momentum of a body is directly proportional to applied force and takes place in the direction of the force
- For every action, there is an equal and opposite reaction
Derivation of the law of conservation of momentum
Let m1, m2 be the masses of two bodies initially moving in the same direction with velocities u1 and u2 which collide after time t, and gain velocities v1 and v2 respectively when u1 > u2.
During collision, each body exerts a force of impact on each other according to Newton’s second law of motion.

Let I be the I impulse on A, then the impulse on B = -I.
I = M1v1 –m1u1 …………….. (i)
-I= m2v2 – m2u2 …………….. (ii)
Equation (i) + equation (ii)
0 = M1v1 –m1u1+ m2v2 – m2u2
m1u1 + m2u2 = m1v1 + m2v2
Alternatively

(d) A body of mass 800kg moving at 30ms-1 collides with another of mass 400kg moving in the same direction at 25ms-1. The two bodies stick together after collision. Calculate the
(i) common velocity just after collision (02marks)
m1u1 + m2u2 = (m1+ m2)v
(800 x 30) + (400 x 25) = (800 + 400)V
v = 28.3ms-1
(ii) kinetic energy lost during collision (03marks)
Kinetic energy lost = kinetic energy before – kinetic energy after
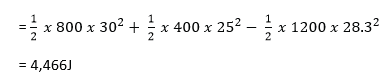
- (a) Define moment of force and give its SI unit. (02marks)
Moment of force is the product of force and perpendicular distance from the line of action of the force to the pivot. S.I units Nm.
(b) Explain briefly how to locate the centre of gravity of an irregular sheet of cardboard. (04marks)
- three holes are drilled around the edge of the cardboard.
- The cardboard is suspended from a pin through one of the holes. When the cardboard is freely suspended, a plumb line is suspended from the same pin.
- A line is drawn to mark the line where the plumb line passes.
- The procedure is repeated for the other two holes.
- The point of intersection of the three line is the centre of gravity
(c) State the conditions necessary for equilibrium of a rigid body under action of a system of forces. (02marks)
- The sum of clock wise moments about a fixed point is equal to the sum of anticlockwise moments about the same point.
- The sum of all the forces acting on the body must be zero. This ensures that the body does not undergo any linear acceleration. Mathematically, this can be expressed as: ∑F = 0
(d) A wheel of radius 0.5m rests on a level surface at point C and makes contact with edge E of a block height 0.2m as shown in the figure below.
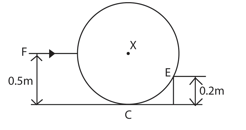
A force F is applied horizontally through the axle of the wheel at X to just move the wheel over the block. If the weight of the wheel is 180N, find the
(i) Force exerted at point E (02marks)

Rsinθ = 180
![]()
R = 300N
The force exerted = 300N
(ii) Force F (04marks)
F – Rcosθ = 300cos 69.90 = 240N
(e) State the laws of friction and explain each of them (06marks)
- Friction force oppose relative motion between surfaces in contact.
Explanation; surfaces have projections with small area. When in contact, the surfaces rest on each other’s projection. Because of the actual area of contact being small, high pressures exist at the points of contact and a force which opposes motion is developed.
- Friction force is independent of area of contact provided normal reaction is constant.
Explanation; When the object is turned over so that different surfaces are presented, the actual area of contact is approximately the same
- The friction force is directly proportional to the normal reaction.
Explanation; when the load increases, the pressure at points of contact increases the actual area of contact producing stronger bonds and increases the degree of interlocks. A greater force is therefore required for motion to take place.
- (a) Define the following as applied to circular motion:
(i) Centripetal acceleration (01mark)
Centripetal acceleration is the rate of change of velocity of a body moving in a circular path.
(ii) Period (01mark)
A period is the time taken to move once round a circular path
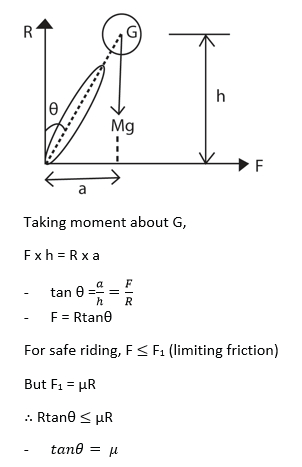
(b) (i) Explain why a cyclist bends inward while going round a curved path. (03marks)
A cyclist bends inwards while going round a curved path to counterbalance centripetal force provided by friction between the tyres and the road such that skidding does not occurs.
The relationship between the lean angle (θ), the speed (v), and the radius of the curve (r) can be expressed as:
tan θ = v2/rg where g = acceleration due to gravity.
(ii) Show that if θ is the angle of inclination of the cyclist to the vertical and μ is the coefficient of limiting friction between the ground and the bicycle tyres, then for safe riding tan θ = μ. (04marks)
(iii) A body of mass 1.5kg moves once round a circular path to cover 44.0cm in 5s. Calculate the centripetal force acting on the body. (04marks)
Radius of circular path, r
Circumference = 2πr = 44cm
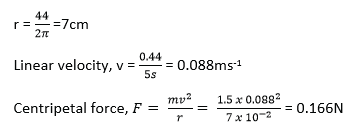
(c) Define simple harmonic motion (01mark)
Simple harmonic motion is the motion of a body whose acceleration is directed towards a fixed point and is directly proportional to the displacement of the body from a fixed point.
(d) A body executes simple harmonic motion with amplitude A and angular velocity, ω.
(i) Write down the equation for velocity of the body at a displacement x from the mean position (01mark)
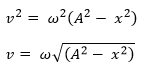
(ii) Sketch the velocity-displacement graph for the body in (d)(i) for ω< 1. (02marks

(iii) If the body moves with amplitude 14.142 cm, at what distance from the mean position will be kinetic energy equal to potential energy? (03marks)
Kinetic energy = half of total energy

- (a) State and illustrate Archimedes’ principle. (05marks)
Archimedes’ Principle: when a body is wholly or partially immersed in a fluid, it experiences an up thrust force equal to the weight of the fluid displaced.

FC = h1ρgA, FD = h2ρga
Net force (up thrust) = (h2-h1)ρgA
Volume of liquid displace = h2-h1)A
Weight of liquid displaced = h2-h1)ρgA
Hence up thrust = weight of liquid displaced
(b)(i) State the law of flotation (01 marks)
A floating body displaces its own weight of fluid in which it floats.
(ii) Describe an experiment to verify the law in (b)(i). (05marks)

- Overflow can is filled with water up to spout level
- An object is lowered in the can until it floats.
- The displaced water is collected in the beaker.
- The weight of the displaced water is determined and found to be equal to the weight of the object.
(c) (i) Write Bernoulli’s equation and define each term in the equation. (02marks)

(ii) Explain the origin of lift force on the wings of a plane. (03marks)

- Air flows above the wing of a plane at high velocity hence low pressure.
- Below the wings, air flows at low velocity and hence high pressure.
- The difference in pressure cause a lift force, therefore net upward force.
(iv) Air flows over the upper surfaces of the wings of an aeroplane at a speed of 120ms-1, and past the lower surface of the wings at 110ms-1.Calclate the lift force on the aeroplane if it has a total wing area of 20m2. Density of air = 1.29kgm-3)
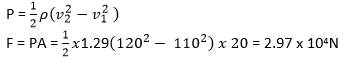
- (a) What is meant by relative velocity? (01mark)
Relative velocity is the velocity of a body moves as observed from another body.
(b) A ship is heading due to north at a speed of 30ms-1. Water in the lake is moving in the north-east direction at an average speed of 5kmh-1. Calculate
(i) relative velocity of the ship (04 marks)
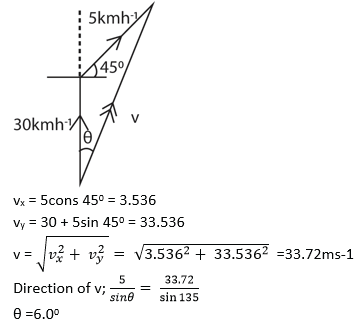
(ii) distance off course the ship will be after 40 minutes. (02marks)
Distance, d = vxt = 5sin450 x = 2.36km
(c) (i) Explain why a passenger in a car jerks forward when the brakes are suddenly applied. (03marks)
When a car is moving forward, both the car and the passengers inside it are traveling at the same speed. When the driver suddenly applies the brakes, the car decelerates rapidly due to the friction between the brakes and the wheels. However, the passengers’ bodies, due to inertia, tend to continue moving forward at the original speed.
(ii) Use Newton’s second law to define the Newton. (04marks)
Consider a body of fixed mass, m acted on by constant force F and its velocity changes from u to v in time, t.

The newton is a force which gives amass of kg an acceleration of 1ms-2.
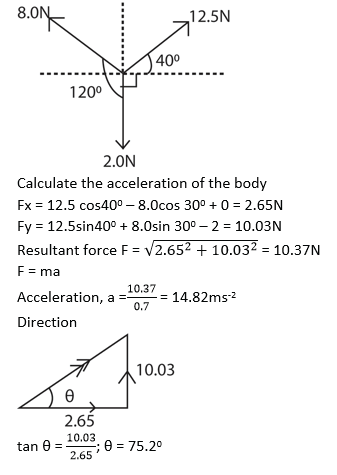
(d) Three forces of 8.0N, 12.5N and 2.0Nact on a body of mass 0.7kg as shown below
Calculate the acceleration of the body
- (a) what is meant by the centre of the mass? (01mark)
Centre of the mass is a point at which the whole mass of a body is considered to be concentrated.
(b) Explain why a long spanner is preferred to a short on undoing a tight bolt. (03marks)
A long spanner is preferred over a short one for undoing a tight bolt due to the concept of torque. Torque is a measure of the rotational force applied to an object and depends on two factors: the amount of force applied and the distance from the pivot point (in this case, the bolt).
Mathematical Explanation
The torque τ can be calculated using the formula:
τ=F×r
where:
- τ is the torque,
- F is the applied force, and
- r is the distance (lever arm) from the pivot point to where the force is applied.
Since a long spanner has long distance r, less effort is required compared when using a shorter spanner
(c) A uniform ladder of length 10m and weight 400N, leans against a smooth wall and its foot rests on rough ground. The ladder makes an angle of 600 with the horizontal. If the ladder just slips when a person of weight 800N climbs 6m up the ladder, calculate the
(i) reaction on the wall and the ground (05marks)
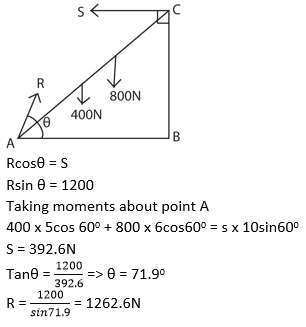
(ii) distance another person of weight 600N can climb up the ladder so that the same reaction are exerted as in (c)(i). (02marks)
400 x 5cos 600 + Lcos600 x 600 = 392.6 x 10sin 600
L= 0.8m
(d) (i) State the principle of conservation of energy. (01mark)
Energy can neither be created nor destroyed but can be changed from form to another.
(ii) How does the principle in (d)(i) apply to a child sliding down an incline? (02marks)
Moving down an incline; potential energy is changed to kinetic energy to heat and sound
(e) A pump with power output of 147.1W can raise 2kg of water per second through a height of 5m and delver it into a tank. Calculate the speed with which the water is delivered into the tank. (03marks)
Power x time = kinetic energy of water + potential energy
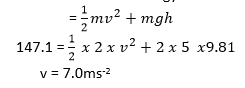
(f) Explain the effect of a couple on a rigid body. (03marks)

A couple consists of two parallel forces that are equal in magnitude, opposite in sense and do not share a line of action
- (a) What is meant by a
(i) Brittle material (01mark)
A brittle material is a substance that breaks easily when a force is exerted on it e.g. glass
(ii)Ductile material (01marks)
A ductile material is one that can be hammered, rolled or moulded into different shapes.
(b) Give one example of each of the materials in (a) (01mark)
Brittle material: glass, clay, cast iron, stone
Ductile material: copper, aluminium
(c) Explain why bicycle frame are hollow (02mark)
Bicycle frame is hollow to reduce weight while maintain strength. A tube is significantly tougher to bend than a rod.
(d) (i) Sketch a labelled graph of stress against strain for a ductile material (02marks)
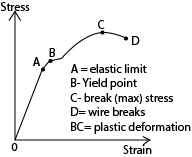
(ii) Explain the main features of the graph in (d)(i) (04marks)
- OA – stress is proportional to strain and the material regains its length
- AB – stress is not proportional to strain but the material regains its length
- Beyond B the material becomes permanently stretched
- CD the material undergoes plastic deformation
- Beyond D the material breaks
(e) Derive the expression for the energy stored per unit volume in a rod of length, L, Young’s Modulus, Y, when stretched through distance, e. (04marks)

(f) A load of 5kg is placed on top of a vertical brass rod of radius 10mm and length 50cm. if
(i) decrease in length (03marks)

(ii) energy stored in the rod. (02marks)
![]()
- (a) Define the following:
(i) Angular velocity
Angular velocity is the rate of change of angular displacement.
(ii) Period
Period is the time taken to make one complete oscillation
(b) An object moves in a circular path of radius, r, with a constant velocity, V. Derive an expression for its acceleration. (04marks)

The velocity change from a to B = vB – vA or vB + (-vA).
In figure above, PQ represents vB in magnitude (v) and direction BD; QR represents -vA in magnitude (v) and direction (CA).
Velocity change = vB + (-vA) = PR
When δt is small, the angle AOB or δθ is small;
Also angle PQR equal to δθ is small
PR or acceleration then points toward O, the centre of the circle.

(c) (i) State two factors on which the rate of flow of a fluid through a tube depends. (02marks)
- viscosity of fluid
- diameter/radius or cross sectional area of the tube
- pressure difference between its end
(ii) Describe an experiment to measure the coefficient of viscosity of a liquid using Poiseulle’s formula

- the liquid of density, ρ, passes slowly from a constant head tank through a capillary tube of length, l and radius r.
- for a height, h, of the tube, the volume V is collect in time t.
- the flow rate R = V/t is calculated
- the experiment is repeated for different value of V and h.
- a graph of R against h is plotted and slope S is obtained
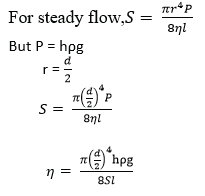
(d) Find the time take for an oil drop of diameter 6.0 x 10-3mm to fall through a distance of 4.0 cm in air of coefficient of viscosity 1.8 x 10-5Pa.
[The density of oil and air are 8.0 x 103kgm-3 and 1kgm-3 respectively]

- (a) (i)State Newton’s laws of motion. (03marks)
- A body continues in its state of rest or uniform motion in a straight line unless acted upon by an external force
- The rate of change of momentum of a body is directly proportional to applied force and takes place in the direction of the force
- For every action, there is an equal and opposite reaction
(ii) A molecule of a gas contained in a cube of side L strikes the wall of the cube repeatedly with a velocity u. Show that the average force F on the wall is given by
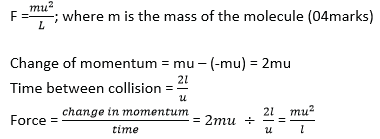
(b) (i) Define linear momentum and state the law of conservation of linear momentum. (02marks)
- Linear momentum is the product of mass and its velocity
- The law of conservation of linear momentum: if the resultant force on a system of interacting bodies is zero; total linear momentum is conserved.
(ii) A body of mass m1 moving with velocity u, collides with another body of mass m2 at rest. If they stick together after collision, find the common velocity with which they move (04marks)
Initial momentum = m1u + m2 x 0 = m1u
Final total momentum = (m1 + m2)v
By conservation of linear momentum
m1u = (m1 + m2)v
![]()
(c) A bullet of mass 10g is fired horizontally with a velocity of 300ms-1 into a block of wood of mass 290g which rests on a rough horizontal floor. After impact, the block and the bullet move together and come to rest when the block has travelled a distance of 15m. Calculate the coefficient of sliding friction between the block and the floor. (07marks)

- (a) State Kepler’s laws of planetary motion. (03marks)
- Planets describe ellipses about the sun as one focus
- The imaginary line joining the sum and planet sweeps out equal areas in equal time intervals
- The square of the periodic time of revolution of planets about the sun are proportional to the cubes of their mean distance from the sun
(b) Use Newton’s law of gravity to derive the dimension of the universal gravitational constant (03marks)

(c) A satellite is resolving at a height, h, above the surface of the earth with period T.
(i) Show that the acceleration due to gravity, g, on the earth’s surface is given by
![]() where re is the radius of the earth. (06marks)
where re is the radius of the earth. (06marks)
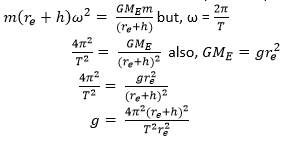
(ii) What is meant by parking orbit? (02marks)
Parking orbit of a satellite that it appears to be stationary to the observer on the earth’s surface. The period of revolution of the satellite is equal to the period of revolution of the earth; i.e. T = 24hours
(d) A satellite revolves in a circular orbit at a height of 600kmabove the earth’s surface. Calculate the
(i) speed of the satellite. (03marks)
![]()
(ii) period of the satellite. (03marks)
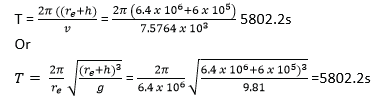
- (a)(i) Define Simple harmonic motion. (01mark)
Simple harmonic motion is the periodic motion of a body whose acceleration is directly proportional to the displacement of a body from a fixed point and it is directed towards the fixed point.
(ii) Sketch a displacement-time graph for a body performing simple harmonic motion. (01mark)

(b) A uniform cylindrical rod of length 16cm and density 920kgm-3 floats vertically in a liquid of density 1000kgm-3. The rod is depressed through a distance of 7mm and then released.
(i) Show that the rod performs simple harmonic motion (06marks)

- Let A be the cross section area of the rod and ρ be the density of the liquid
- Weight of the liquid displaced = up thrust.
- The volume of the liquid displaced = AL and therefore up thrust, u = ALρg
- When the rod is slightly displaced through a distance x, the new up thrust,u’ = A( L+ x)ρg
- Resultant force, F + ALρg – A( L+ x)ρg = – Aρgx
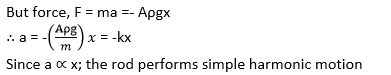
(ii) Find the frequency of the resultant oscillations. (04marks)
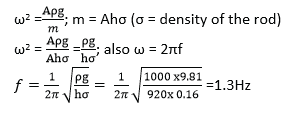
(iii) Find the velocity of the rod when is at a distance of 5mm above the equilibrium position (03marks)
![]()
(c) What is meant by potential energy? (01mark)
Potential energy is the energy possessed by the body by the virtue of its position or state
(d) Describe the energy changes which occur when a
(i) ball thrown upwards in air (03marks)
Chemical energy →P.E → K.E + P.E → P.E → K.E + P.E → K.E → sound + heat
(ii) loud speaker vibrating (01mark)
Electrical energy → mechanical energy → sound
- (a)(i) Define elastic deformation and plastic deformation (02marks)
- Elastic deformation is when a material is deformed and it regains its original shape and size when the deforming force is removed.
- Plastic deformation occurs when a force is applied and the material does not regain its original shape and size when the force is removed
(ii) Explain what is meant by work hardening. (02marks)
Work hardening is the strengthening of a material by repeatedly deforming it. Atomic planes slide over each other, this increases plane dislocations which prevent further sliding of planes.
(b) (i) Sketch using the same axes, stress-strain curves for ductile material and for rubber (03marks)

(ii) Explain the features of the curve for rubber. (03marks)
Rubber does not obey Hooke’s law except for a very small range; it stretches easily without breaking and has a greatest range of elasticity. It does not undergo plastic deformation
Unstretched rubber consist of coiled molecules when a tensile force is applied, they uncoil, become straight and hard. Any further increase in tensile force makes the rubber to break.
(c) A capillary tube is held in a vertical position with one end dipping in a liquid of surface tension γ and density ρ. If the liquid rises to a height, h, derive an expression for h in terms of γ, ρ and radius r of the tube assuming the angle of contact is zero. (04marks)
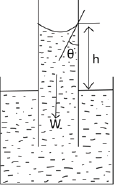
The liquid rises until the vertical component of the upward forces due to surface tension is equal to the weight of the liquid column.
Fγcosθ = W but θ = 0
=> Fγ = W
![]()
F = γL
L = 2πr
But W = mg and m = Vρ (where ρ is the density of the liquid in kg/m3)
W = vρg = 2πr2hρg
Fγ = 2πr2hρg
γ.2πr =2πr2hρg
![]()
γ – coefficient of surface tension
θ – angle of contact
r – radius of capillary tube
ρ – density of the liquid
(d) A mercury drop of radius 2mm falls vertically and on hitting the ground, it splits into two drops each of radius 0.5mm. Calculate the change in surface energy given that the surface tension of mercury is 0.52Nm-1. (05marks)
Surface area of a drop = 4πr2
Surface area of a big drop = 4π(0.002)2 = 5.03 x 10-5m2
Surface area of two small drops = 2 x 4π(0.0005)2 = 6.28 x 10-6m2
Change in area = 5.03 x 10-5 – 6.28 x 10-6m2 = 4.402 x 10-5m2
Change in surface energy = change in area x coefficient of surface tension
= 4.402 x 10-5 x 0.52
= 2.289 x 10-5J
(e) State the effect of temperature on surface tension of a liquid. (01mark)
Increase in temperature lowers surface tension
- (a) (i) Define dimensions of a physical quantity. (01mark)
Dimensions of a physical quantity is the way it is related to fundamental quantities; mass, length and time
(ii) In the gas equation
![]()
Where P = pressure, V= volume, T= absolute temperature and R= gas constant, what are the dimensions of the constants a and b? (04mark)


(c) (i) Define elastic limit of a material. (01marks)
Elastic limit is the maximum load which a material can experience and still regain its original size and shape once the load has been removed.
(ii) Describe an experiment to determine Young’s Modulus of a steel wire. (06marks)
Experiment to determine Young’s Modulus for a metal wire

- Two thin, long wires of the same material and length P and Q are suspended from a rigid support.
- P carries a scale M in mm and it’s straightened by attaching a weight at its end.
- Q carries a Vernier scale which is alongside scale M
- Various loads are added to the test wire and corresponding extensions caused are read off from a Vernier scale.
- The diameter (2r) of the wire is obtained by a micrometre screw gauge, and the cross section area of the wire A = 4πr2
- A graph of mass (m) of the load against extension e is plotted

![]()
(d) Explain why tyres of a vehicle travelling on a hard surfaced road may burst. (04marks)
When the car moves on a hard surface, friction between the tyres and the surface causes heating and the temperature inside the tyres increase. The increase in temperature increases the pressure inside the tyre which may lead to bursting.
- (a) (i) What is meant by efficiency of a machine? (01mark)
Efficiency is the ratio of useful work done by a machine to the energy used by the machine; (expressed as percentage)
(ii) A car of mass1.2 x 103kgmovesup an incline at a steady velocity of 15ms-1 against a frictional force of 6.0 x 103N. The incline is such that the car rises 1.0m for every 10m along the incline. Calculate the output power of the car engine. (04marks)
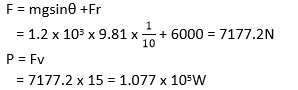
(b) (i) Define the impulse and momentum. (02marks)
- Impulse is a product of force and time of action of the force
- Momentum is a product of mass and its velocity
(ii) An engine pumps water such that the velocity of the water leaving the nozzle is 15ms-1. If the water jet is directed perpendicularly on a wall and comes to a stop at the wall, calculate the pressure exerted on the wall. (03marks)
Force exerted on the wall, F = ρAV2
![]()
(c) (i) Define inertia. (01mark)
Inertial is the reluctance of a body to start moving once at rest or to stop moving once it has begun to move.
(ii) Explain why a body placed on a rough plane will slide when the angle of inclination is increased. (04marks)

A body of mass, m placed on a plane inclined at an angle θ above the horizontal has its component mgsinθ downwards along the plane. Since the plane is rough, mgsinθ causes the frictional force Fr which prevents the body from sliding.
As θ increases, mgsinθ exceeds maximum Fr and the body slides.
(d) (i) State the conditions for a body to be in equilibrium under action of coplanar forces. (02marks)
- Resultant force on the body is zero
- Algebraic sum of moments at any point is zero.
(ii) Briefly explain the three states of equilibrium (03marks)
- When a body in stable equilibrium is slightly displaced, its centre of gravity is raised. When released, it returns to its original position.
- When a body in stable equilibrium is slightly displaced, its centre of gravity is lowered and it continues to fall on release- topples.
- For neutral equilibrium, the centre of gravity remains the same on displacement.
- (a) (i) What is meant by conservative forces? (01mark)
A conservative force is one for which the work done to move a body from one point to another is independent of the path taken and only depends on initial and final position of the body.
(ii) Give two examples of conservative forces (02marks)
- Mechanical energy
- Work done to move the body round a closed path.
(b) Explain the following
(i) damped oscillations (02marks)
Damped oscillation are oscillations in which the oscillatory system loses energy to the surroundings due to dissipative forces. The amplitude of the oscillations reduces with time.
(ii) Forced oscillations (02marks)
Force oscillations are those which are maintained by external force.
(c) (i) State Newton’s law of gravitation (01mark)
Newton’s law of gravitation states that every particle of matter attracts every other particle with a force which is directly proportional to the product of their masses and inversely proportional to the square of their distance apart.
(ii) Show that Newton’s law of gravitation is consistent with Kepler’s third law. (05marks)
Consider a planet of mass MP moving around the sun of mass MS in a circular orbit of radius r.
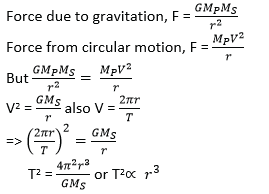
(d) If the earth takes 365 days to make one revolution around the sun, calculate the mass of the sun (04marks)
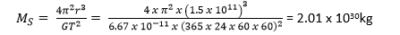
(e) Explain briefly how satellites are used in world-wide radio or television communication. (04marks)

- A set of satellites is launched in parking orbit as shown in the diagram above.
- A radio signal from A is transmitted to a geosynchronous satellite 1
- The signals are retransmitted from satellite 1 to geosynchronous satellite 2, then to 3 and finally to B.
- (a) (i) What is meant by fluid element and flow line as applied to fluid flow? (02mark)
- A fluid element is a molecule (the smallest volume) of the fluid which follows the flow.
- A flow line is the path which individual molecule in a fluid element describes.
(ii) Explain why some fluids flow more easily than others (03marks)
Fluid flow involves different parts of a fluid moving at different velocities. Different parts of the fluid therefore slide past each other in layers. There exists frictional force between the layers which affects the flow rate. Liquids with low friction or viscosity flow faster than those with high viscosity.
(b) (i) state Bernoulli’s Principle. (01mark)
Bernoulli’s Principle states that for a streamline motion of an incompressible non viscous fluid, the sum of pressure at any point, the kinetic energy per unit volume is always constant.
(ii) Explain how a Pitot-static tube works (04marks)
Setup

Pitot-static tube consists of a static tube which measure the static pressure and the pilot tube that measures the total pressure. Total pressure is the sum of static and dynamic pressure.

(c) Air flowing over the upper surface of an air craft’s wing causes a lift force of 6.4 x 105N. The air flows under the wing at a speed of 120ms-1 over an area of 28m2. Find the seed of air flow over an equal area of the upper surface of the air craft’s wings. [Assume density of air = 1.2kgm-3) (04marks)
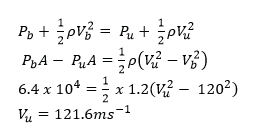
(d) (i) What is meant by surface tension and angle of contact of a liquid? (02marks)
- Surface tension is the force per metre length acting in the surface at right angles to one side of the line drawn in the surface.
- Angle of contact is the angle between the solid surface and the tangent plane to the liquid surface measured through the liquid.
(ii) A water drop of radius 0.5cm is broken up into other drops of water each of radius 1mm. assuming isothermal conditions, find the total work done to break up the water drop. (04marks)

- (a) (i) what is meant by conservative force? (01mark)
Conservative force are forces for which the work done in moving a body around a closed path is zero.
Or
Conservative force is the one for which the work done in moving a body from one point to another is independent of the path taken.
(ii) Give two examples of conservative forces. (01mark)
Gravitational force, magnetic force, electric force, elastic force
(b) (i) State the law of conservation of mechanical energy. (01mark)
The sum of kinetic energy and potential energy is constant in the absence of dissipative forces.
(ii) A body of mass, m, is projected vertically upwards with speed, u. show that the low of conservation of mechanical energy is obeyed throughout its motion. (05marks)

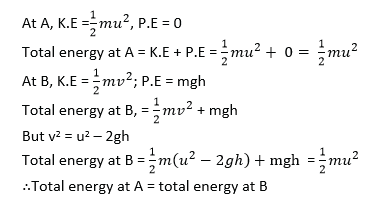
(iii) Sketch a graph showing variation of kinetic energy by the body with time. (01 mark)

(c) (i) Describe an experiment to measure the coefficient of static friction. (04marks)

- A block of mass m is placed on a flat table and connected to a scale pan as shown in the diagram above.
- Small weights are added in bits on to the scale pan until the block just starts to move. The total weight of the scale pan and weights added is obtained, Wf.
- The coefficient of static friction is given by
![]()
Alternative method

- A block is placed on horizontal plane. The plane is tilted gently until the block just start to slide
- The angle of tilt θ is measured
- The coefficient of static friction, μ = tanθ
(ii) State two disadvantages of friction. (01mark)
- Wastes energy
- Causes wear and tear
- Causes noise
- Generates unnecessary heat
(d) A bullet of mass 20g moving horizontally strikes and get embedded in a wooden block of mass 500g resting on a horizontal table. The block slides through a distance of 2.3m before coming to rest. If the coefficient of kinetic friction between the block and table is 0.3, calculate
(i) friction force between the block and the table. (02marks)
F = μmg = 0.3 x 0.52 x 9.81 = 1.53N
(ii) velocity of the bullet just before it strikes the block. (04marks)

- (a) (i) State the principle of moments. (01mark)
When a body is in mechanical equilibrium, the sum of clockwise moments about any point is equal to the sum of anticlockwise moments about the same point
(ii) Define the terms centre of gravity and uniform body. (02marks)
- Centre of gravity is the point where the resultant force on the body due to gravity acts.
- A uniform body is one whose centre of gravity is the same as the geometrical centre.
(b) Figure below shows a body, M of mass 20kg supported by a rod of negligible mass horizontally hinged to a vertical wall and supported by a string fixed at 0.5m from the other end of the rod.
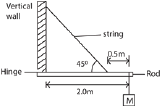
Calculate the
(i) Tension in the string (03marks)

Tsin45 x 1.5 = 20 x 9.81 x 2
T = 370N
(ii) Reaction of the hinge (03marks)
Rcosθ = 370cos 45 ………………(i)
Taking moments about O
Rsinθ x 1.5 = 20 x 9.81 x 0.5 …. (ii)
Eqn. (i) and (ii)
θ = 140
(iii) Maximum additional mass which can be added to the mass of 20kg before the string can break given that the string cannot support a tension of more than 500N. (02marks)
Taking moments about the hinge
500sin 45 x 1.5 =X x 9.81 x 2
X = 27kg
extra mass = 27 – 20 = 7kg
(c) (i) Define Young’s modulus. (01marks)
Young’s modulus is the ratio of tensile stress to tensile strain
(ii) Explain the precautions taken in determinations of Young’s modulus of a wire. (06marks)
- After each reading, the load is removed to check that the wire returns to its original length, to ensure that elastic limit is not exceeded.
- Long wires are used to achieve measurable expansion
- Thin wires are used to produce high tensile stress
- Identical wires are used to eliminate error of expansion or contraction due to changes in temperature.
(iii) Explain why a piece of rubber stretches much more than a metal wire of the same length and cross section (02marks)
Rubber consist of coiled molecules while metal does not. When load is applied to rubber, the molecules uncoil leading to a larger extension
- (a) State Kepler’s laws of planetary motion (03marks)
- Planets resolve in elliptical orbits with the sun at the focus.
- The imaginary line joining the sun to any planet sweeps out equal areas in equal time intervals
- The square of the period of revolution of a planet is proportional to the cube of the mean distance from the sun to planet
(b) (i) what is a parking orbit? (01mark)
A parking orbit is the path in space followed by a satellite whose period of revolution is equal to the period of rotation of the earth.
(ii) Derive an expression for the period, T, of a satellite in a circular orbit of radius, r, above the earth in terms of mass of earth, m, gravitational constant, G and r. (04marks)
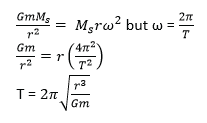
(c) (i) A satellite of mass 200kg is launched in a circular orbit at a height of 3.59 x 107m above the earth’s surface. Find the mechanical energy of the satellite. (03marks)
![]()
(ii) Explain what will happen to the satellite if its mechanical energy was reduced. (03marks)
When mechanical energy, M.E is reduced, the satellite falls to orbit of smaller radius
(d) Describe laboratory method of determining the universal gravitational constant, G. (06marks)
Determining gravitational constant

- Two equal lead spheres A and B each of mass, m, are attached to end of a bar AB of length, L.
- The bar AB is suspended from a ceiling.
- Large spheres P and Q are brought towards A and B respectively from the opposite side
- Large spheres P and Q altered small spheres A and B respectively by equal and opposite gravitational forces give rise to gravitational torque, F, which in turn twist the suspended through angle θ.
- A resting torque of the wire opposes the twisting of the wire from equilibrium position
Then
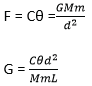
Where
d = distance between the centre of A and P or B and Q.
C = The twisting couple per unit twist (θ = 1)
- (a) (i) Distinguish between surface tension and surface energy (01mark)
- Surface tension is a force per unit length acting at right angle to one side of an imaginary line drawn in the liquid surface
- Surface energy is the work done in increasing area of the surface by 1m2 under isothermal conditions.
(ii) Show the surface energy and surface tension are numerically equal. (03marks)
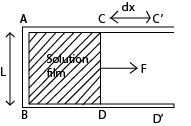
- F a wire frame ABCD is put in a solution of surface tension γ and a film of the solution forms on ABCD; and if a force F is used to extend the film to ABC’D’ ;
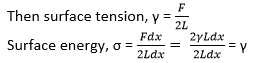
Thus, surface energy, σ = surface tension, γ
(iii) Explain why water dripping out of a tap does so in spherical shapes. (03marks)
For any given volume, a sphere is a shape that offer minimum surface area and therefore the most stable
(b) Two soap bubbles of radius 2.0cm and 4.0cm respectively coalesce under isothermal conditions. If the surface tension of the soap solution is 2.5x 10-2Nm-1, calculate the excess pressure inside the resulting soap bubble. (04marks)
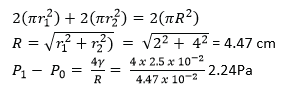
(c) (i) State Bernoulli’s principle (0marks)
Bernoulli’s Principle states that for a streamline motion of an incompressible non viscous fluid, the sum of pressure at any point and kinetic energy per unit volume is always constant.
(ii) Explain how wind at a high speed over the roof of a building can cause the roof to be ripped off the building. (03marks)
Wind blowing at a high speed over the roof of a building causes pressure above the roof to decrease below the pressure in the building where the wind is slow. This difference in pressure causes a resultant force that pushes the roof off the building.
(iii) An aeroplane has a mass of 8,000kg and wing area of 8.0m2. When moving through still air, the ratio of its velocity to that of the air above its wings is 0.25. At what velocity will the aeroplane be able to just lift off the ground? (Density of air = 1.3kgm-3)
- Minimum force to lift an aeroplane = 8000 x 9.81 = 78480N
- If v is the velocity of the aeroplane, then velocity of air below the wings vb = v.
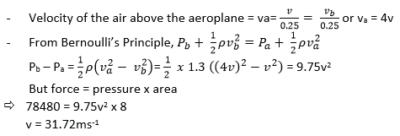
- (a)(i) What is projectile motion? (01 marks)
Projectile motion is motion of the body which after being given an initial velocity moves under the influence of gravity.
(ii) A bomb is dropped from an aeroplane when it is directly above a target at a height of 1402.5m. The aeroplane is moving horizontally with a speed 0f 500kmh-1. Determine whether the bomb will hit the target. (05marks)

(b) (i) Define angular velocity. (01mark)
Angular velocity is the rate of change of angle for a body moving in a circular path.
(ii) a satellite is revolving around the earth in a circular orbit at an altitude of 6 x 105m where the acceleration due to gravity is 9.4 ms-2. Assuming that the earth is spherical, calculate the period of the satellite. (03marks)
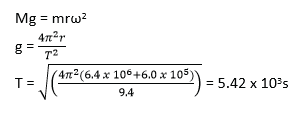
(c) (i) State Newton’s laws of motion (03marks)
- A body continues in its state of rest or uniform motion in a straight line unless acted upon by an external force
- The rate of change of momentum of a body is directly proportional to applied force and takes place in the direction of the force
- For every action, there is an equal and opposite reaction
(ii) Explain how a rocket is kept in motion. (04marks)
Fuel is burst in a combustion chamber and exhaust gases are expelled at high velocity. This causes a large backward momentum. From the principle of conservation of linear momentum, an equal forward momentum is gained by the rocket.
Due to continuous combustion of the fuel, there is a large change in forward momentum which lead to the thrust, hence maintaining the motion of the rocket.
(iii) Explain why passengers in a bus are thrown backwards when the bus suddenly start moving (03marks)
Passengers are thrown backwards because of inertia. When the bus sets off the passenger tend to stay at rest because the force acts on the bus does not act on the passengers.
- (a) (i) What is meant by Young’s modulus? (03marks)
Young’s Modulus is the ratio of tensile stress to tensile strain of a material
(ii) State Hooke’s law (01mark)
Hooke’s law states that the extension of a material is proportional to the stretching force provided the elastic limit is not exceeded.
(iii) Derive an expression for energy released in a unit volume a stretched wire in terms of stress and strain. (04marks)
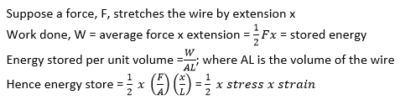
(b) A steel wire of length 0.6m and cross-section area 1.5 x 10-6m2 is attached at B to a copper wire BC of length 0.39m and cross section area 3.0 x 10-6m2. The combination is suspended vertically from a fixed point at A and supports a weight of 250N at C. find the extension in each of the wires, given that Young’s Modulus for steel is 2.0 x 1011Nm-2 and that of copper is 1.3 x 1011Nm-2. (05marks)
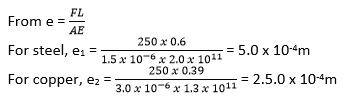
(c) With the aid of a labelled diagram, describe an experiment to determine the Young’s Modulus of a steel wire (07marks)
Experiment to determine Young’s Modulus for a metal wire

- Two thin, long wires of the same material and length P and Q are suspended from a rigid support.
- P carries a scale M in mm and it’s straightened by attaching a weight at its end.
- Q carries a Vernier scale which is alongside scale M
- Various loads are added to the test wire and corresponding extensions caused are read off from a Vernier scale.
- The diameter (2r) of the wire is obtained by a micrometre screw gauge, and the cross section area of the wire A = 4πr2
- A graph of mass (m) of the load against extension e is plotted

![]()
(d) Explain the term plastic deformation in metals (02marks)
During plastic deformation, some crystal planes slide over each other. The movement of dislocation takes place and on removing the stress, the original shape and size are not recovered due to energy loss in form of heat.
- (a) Define work and energy (02marks)
Work is a product of force and distance moved in the direction of force.
Energy is the ability to do work
(b) Explain whether a person carrying a bucket of water does any work on the bucket while walking on a levelled road. (03marks)
There is no net force on the bucket in horizontal direction. The only force he exerts on the bucket is against the weight mg of the bucket perpendicular to the direction of motion.
From work = Fcos90 = 0, there is no work done on the bucket
(c) A pump discharges water through a nozzle of diameter 4.5cm with speed of 62ms-1 into a tank 16m above the intake.
(i) Calculate the work done per second by the pump in raising the water if the pump is ideal. (04marks)
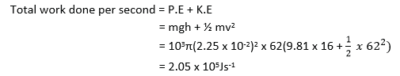
(ii) Find the power wasted if the efficiency of the pump is 73% (02marks)

(iii) Account for the power loss in (c)(ii) (02marks)
Power is lost in overcoming friction and some is converted into sound and heat
(d) (i) State work-energy theorem. (01mark)
It states that work done by the net force acting on a body is equal to the change in its kinetic energy.
(ii) Prove the work-energy theorem for a body moving with constant acceleration. (03marks)

Therefore work done = change in kinetic energy
(e) Explain briefly what is meant by internal energy of a substance. (03marks)
The internal energy of a body or a substance is the total sum of kinetic energy and potential energy of the particles of a substance is the internal energy of a substance
Please obtain free notes, exams and marking guides of Physics, chemistry, biology, history, economics, geography … from digitalteachers.co.ug website.
Thanks
Dr. Bbosa Science
Sponsored by The Science Foundation College +256 753 802709

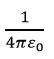 9.0 x 109F-1m
9.0 x 109F-1m
You have a knack for making things clear. Stationary
Your content is a real gem. TamilBlasters Com
Explore the MBBS Fees Structure in Maharashtra for top medical colleges across the state.
Get complete transparency with MBBS Fees Structure in Maharashtra.
Experience top-notch gaming with the easy-to-use Raja Luck App.