Chemical equilibrium

It is a branch of physical chemistry that deals with reversible reactions or reactions that proceed in either direction.

For example, when steam passed over heated iron, hydrogen, and iron (II)diiron (III) oxide is formed. If, however, hydrogen is passed overheated iron (II) diiron (III) oxide, steam and iron are produced. Such reactions are said to be reversible and the equation for this reversible reaction is expressed as follows:

3Fe(s) + 4H₂O(g)     →       Fe₃O₄(s)  + 4H₂ (g)

The direction of the reaction depends on the conditions: if hydrogen gas is removed as fast as it has formed, the reaction proceeds from left to right. Alternatively, if steam is removed as fast as it is formed the reaction will proceed from right to left.

By having steam and iron in a closed vessel, a state is reached at which all the four substance exist in equilibrium but the equilibrium in a balanced reaction is a dynamic one, that is, the substances are still reacting together except that the velocities of the forward and backward reaction are equal.

The equilibrium constant, Kc

The state of equilibrium of a reversible reaction at a given temperature is defined by the equilibrium constant  as follows

For a reaction

3Fe(s) + 4H₂O(g)       ↔       Fe₃O₄(s)  + 4H₂ (g)

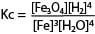
Where [ ] means concentration of the item in moles per litre or moles per dm³

For a general equation

aA + bB     ↔        cC + dD

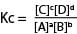
Units of Kc

The units of   are derived by principles of dimension

for instance

Trail 1

Write expressions for Kc for the following reaction and state their units

• N₂+ 3H₂    ↔       2NH₃
• 2NH₃       ↔        N₂+ 3H₂
• N₂  + O₂   ↔       2NO
• C₂H₅OH + HCl     ↔      C₂H₅Cl + H₂O

Implication of Kc

When Kc  is high, it implies that there are more products at equilibrium than the reactants

Application of equilibrium constant, Kc

To calculate the amounts of the reactants and product at equilibrium

Summary of characteristics of equilibrium

• Occurs at constant temperature
• Occurs in closed system
• It is dynamic equilibrium

Example 1

Hydrogen reacts with iodine according to the following equation

H₂(g) + I₂(g)    →  2HI(g)

A mixture of 0.8 moles of hydrogen and 0.6 moles of iodine was allowed to react in a sealed tube at 450⁰C at equilibrium 0.2 moles of iodine had reacted.

(a) Write the expression for the equilibrium constant, Kc, for the reaction

(b)Calculate the value of (2 marks)

First we calculate the moles at equilibrium

mole of I₂ at equilibrium = 0.6 – 0.2 = 0.4 moles

Moles of H₂ at equilibrium

Mole of H₂ that reacted = moles I₂ that reacted    = 0.2moles

Thus, mole of H₂ at equilibrium = 0.8 – 0.2 = 0.6 moles

Moles of HI at equilibrium

1 mole of I₂ that reacted produces 2moles of HI

 0.2 moles of I₂ produced 0.4 mole of HI

Secondly, we substitute in Kc expression

Example 2

When 8.28 g of ethanol were heated with 60 g of ethanoic acid, 49.74 g of the acid remained at equilibrium. Calculate

What mass of ethylethanoate should be present in equilibrium mixture firmed from 13.8 g of ethanol and 12 g of ethanoic acid

Ethanol and ethanoic acid react as follow:

CH₃CH₂OH + CH₃COOH            ↔  CH₃COOCH₂CH₃ + H₂O

ethanol         ethanoic acid             ethylethanoate    water

(H= 1, C = 12, O = 16)

Solution

Relative molecular mass of ethanol, CH₃CH₂OH          = 46

From the reaction equation

Moles of ethanoic      acid that reacted

=

Moles of ethanol that reacted

=

Moles of ethylethanoate that formed

Mole of ethanioic reacted = 1-0.829 = 0.171moles

Moles of water formed = moles of ethanoic acid reacted = 0.171moles

moles of ethanol that remained = 0.18- 0.171

                                                      = 0.009moles

Trial 2

When 6.22moles of hydrogen were heated with 5.71moles of iodine in a sealed tube at 356⁰C it was found that 9.60moles of hydrogen iodide were present at equilibrium. Calculate

(i) the equilibrium constant

(ii) the moles of hydrogen iodide in equilibrium mixture formed by heating 6.41 moles of hydrogen and 10.40 moles of iodine at 356⁰ C

Trial 3

Nitrogen reacts with hydrogen according to the following equation

N₂(g) + 3H₂ (g)    ↔       2NH₃(g)

• Write expression for equilibrium constant, Kc
• Stoichiometric amounts of nitrogen and hydrogen were reacted  in a 2litre vessel. At equilibrium, 0.8moles of ammonia was formed

Calculate

(i) the amount of hydrogen at equilibrium

(ii) the value of equilibrium constant,.

Trial 4

Hydrogen iodide decomposes when heated according to equation

2HI(g)      ↔       H₂(g) + I₂ (g)  ∆H +11.3kJmol^-1

(a) Write an expression for equilibrium constant,  for the reaction (1mark)

(b) 1.54g of HI was heated in a 600cm³ bulb at 530⁰C. When equilibrium was attained, the bulb was rapidly cooled to room temperature and broken down under potassium iodide solution. The iodine formed from decomposition required 67.0cm³ of 0.1M sodium thiosulphate solution.

Calculate

(i) the number of moles of HI in 1.54g (1mark)

(ii) number of moles of iodine formed when hydrogen iodide decomposed (3marks)

(iii) The value of Kc

(c) State what would be the effect on  if

(i) the temperature was raised from 530⁰C to 800⁰C

(ii) the volume of the bulb was increased to 1200cm³.

Trial 5

1mole of H₂ and 1mole of I₂ were introduced into 2litre vessel at temperature at which the equilibrium constant is 55.3. How many moles of H₂, I₂ and HI are there after equilibrium has been established.

Trial 6

A reaction occurs according to the following stoichiometric equation:

A + 2B ↔  2C;

3 moles of A and 5 moles of B were brought together in a volume of 3 litres and after equilibrium has been established, 1 mole of A remained. Calculate the equilibrium constant, Kc.  for the reaction

Trial 7

A reaction occurs according to the following stoichiometric equation:

2A + B     ↔  3C

and has equilibrium constant of 1/10. How many moles of B must be brought into contact with 5 moles of A to produce at equilibrium 5 moles of C.?

Trial 8

5moles of ethanol, 6 moles of ethanoic acid, 6moles of ethylethanoate and 4moles of water were mixed together in a stoppered bottle at 15⁰C. After equilibrium had been attained the bottle was found to contain only 4 moles of ethanoic acid.

(a) (i) Write an equation for the reaction between ethanol and ethanoic acid to form ethylethanoate and water.

(ii) Suggest a mechanism for the reaction

(b) Write an expression for the equilibrium constant, Kc,   for this reaction

(c) How many moles of ethanol, ethanoic acid, ethylethanoate and water are present in the equilibrium mixture?

(d) What is the value for   for this reaction

(e) Suppose 1 mole of ethanol,1 mole of ethanoic acid,3 moles of ethylethanoate and 3 mole of water are mixed together in a stoppered flask at 15⁰ C. How many moles of

(i) ethanol,

(ii) ethanoic acid

(iii) ethylethanoate

(iv) water are present

Equilibrium Constant in terms of, Kp

Watch this

https://youtu.be/_I0-8DonInQ

When at least one of the substances in equilibrium is gases, the state of equilibrium may be defined by equilibrium constant  as follows

For a reaction;

aA(g) + bB(g)   ↔        cC(g) + dD(g)

Application of  Kp

Like Kc, Kp,   is used to predict the proportion of the products and reactants at the equilibrium point in the mixture

Example  3

AT 700⁰C and total pressure of one atmosphere the partial pressure at equilibrium for sulphur dioxide and oxygen are 0.27 and 0.41 atmospheres respectively. Sulphur dioxide is oxidized to sulphur trioxide according to the following equation

2SO₂(g) + O₂(g)   ↔        2SO₃ (g)

Calculate the equilibrium constant, Kp , for the reaction (4 marks)

Solution

Partial pressure of SO₃   = (1-(0.27 + 0.41)

                                                =  0.32atm.

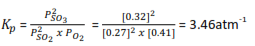
Trial 9

1mole of hydrogen iodide at 25⁰C was introduced into a container of 20 liters

(a) Calculate the pressure of the gas, assuming ideal behavior (1mole of a gas occupies 22.4dm³ under standard conditions).

(b) The sample of hydrogen iodide considered above was raised to a temperature of 300⁰C and partially decomposed into hydrogen and iodine gases; at equilibrium 0.1 mole of iodine was found to be present

(i) Write an equation for decomposition

(ii) Calculate the pressure of the equilibrium mixture at 300⁰C, assuming no volume change.

(iii) Calculate the equilibrium constant at 300⁰C

(c) ∆H⁰_f HI = 26.5kJmol^-1. Explain giving reasons how you would expect the equilibrium constant to change with temperature.

Trial 10

Nitrogen reacts with hydrogen according to the following equation

N₂ (g) + 3H₂(g)     ↔        2NH₃(g)

(a) Write the equation for the equilibrium constant for the reaction in terms of partial pressure and indicate units (2 marks)

(b) Stoichiometric amounts of nitrogen and hydrogen were reacted at 50 atmospheres and at equilibrium, 0.8 moles of ammonia were formed.

calculate

(i) the amount of hydrogen at equilibrium (2½ marks)

(ii) The value of equilibrium constant for the reaction (4 ½ marks)

Trial 11

Consider the following reaction

H₂ (g) + I₂(g)     ↔      2HI (g)

At a certain temperature, analysis of an equilibrium mixture of the gases yielded the following results

(a) Calculate the equilibrium constant for the reaction and state its units.

(b) In second experiment at the same temperature, iodine and hydrogen were mixed together with each gas at a partial pressure of 3 x 10^-1 atm. what are the partial pressures of hydrogen, iodine and HI at equilibrium?

(c) In the third experiment at the same temperature, pure hydrogen iodide was injected into the flask at a pressure of  6 x 10^-1 atm. What are the partial pressures of hydrogen, iodine and hydrogen iodide at equilibrium?

(d) What effect, if any, will decreasing the temperature have on the value of ? Explain your answer.

Trial 12

0.196g nitrogen and 0.146g hydrogen were heated together until equilibrium is established at a given temperature. The pressure found at equilibrium was found to be 90% its value at the beginning. Calculate the percentage composition by volume of the resulting mixture (H = 1, N = 14)

Trial 13

(a)(i) Nitrogen (II) oxide combines with O₂ at 80⁰C and 200atmosphere to form Nitrogen (IV) oxide according to equation

2NO (g) + O₂(g)      ↔     2NO₂(g),  ∆H –xkJmol^-1

(i) Write an expression for the equilibrium constant, Kp,  for the reaction

(ii) Calculate, if the mixture contained 67% nitrogen (IV) oxide (3 ½ marks)

(b) State how the value of Kp will be affected if

        (i) Temperature is increased

        (ii) Catalyst is added

(c) The kinetic data for the reaction in (a) is shown in the table below

Initial rate/ Nm-2s-1	6.8	27.2	61.2	108
P2NO/N2M4	0.04	0.16	0.36	0.64

P_NO =the partial pressure of NO

(i) Plot a graph of initial rate against P²_NO (03mark)

(ii) Using a graph, determine the order of reaction with respect to nitrogen II oxide

(iii) Give a reason for your answer

(d) When the partial of O₂ was doubled to a new constant value, the gradient of the graph in C(i) doubles

(i) Determine the order of reaction with respect to O₂. Explain your answer.

(ii) Write the rate equation for the reaction in (d)

(iii)  Calculate the rate constant when the initial rate is 170Nm^-2s^-1, P_NO = 0.1NM^-2, PO₂ = 1.36Nm^-2

(e) State the effect of the following on the rate of the reaction

(i) Having partial of nitrogen II oxide while that of oxygen is kept constant

(ii) Doubling partial pressure of both nitrogen II oxide and O₂.

Relationship between  and Kc and Kp

We have already seen that equilibrium constants are normally expressed in term of concentration using the symbol  and that, for reaction involving gases; it is usually convenient to express the amount of gases in terms of partial pressure rather than its molar concentration using the Ideal equation

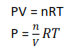
where p is the pressure in atmosphere, n is the number of moles, V, is the volume in cubic decimeter and T is the temperature in Kelvin. In this case R, the gas constant, has units are atmdm^-3K^-1mol^-1

P = [gas]RT

Where [gas] is the concentration of the gas in moldm^-3

Thus, at constant temperature, the pressure of a particular gas is proportional to concentration

i.e. P α  [gas]

This means that for equilibrium

H₂(g) + I₂(g)     ↔      2HI(g)

we can either write

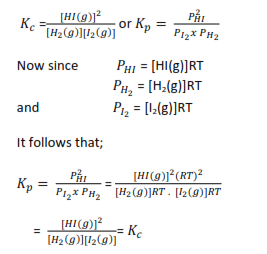
In this particular example Kp = Kc  and neither  nor  has units, but this is not always the case;

Consider another reaction

N₂(g) + 3H₂(g)   ↔         2NH₃(g)

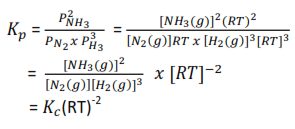
It implies that the numerical value of Kp is the same as that of  Kc only where there are the same number of moles on each side of the Stoichiometric equation.

Although the SI unit of pressure is Nm^-2, it is standard practice to use atmospheres as pressure unit in expressing  Kp values.

In general,  Kp = Kc (RT)^∆n

where ∆n = number moles on the right of the equation minus number of moles on the left.

Example  4

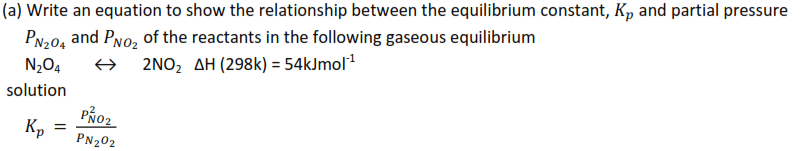
(b) State the effect, if any, on above equilibrium of

(i)  increasing the pressure

Equilibrium shift from right to left leading to reduction in number of moles to fit in small volume.

(ii)  raising the temperature . Give reason for your answer.

Equilibrium shifts from left to right to reduce on the increase in temperature since the forward reaction is endothermic.

(c) It was found that one dm³ of the gaseous mixture weighed 2.777g at 50⁰C and pressure of 1.01 x 10^-5Nm^-2 (1 atmosphere)

Calculate

(i) The fraction of N₂O₄ that dissociated

solution

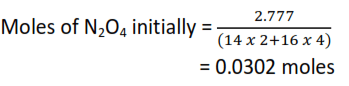
Moles at equilibrium

From ideal gas equation, PV = nRT

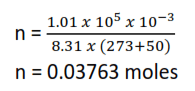
If α is the fraction ionizes

Then

[1 mole of a gas occupies 22.4dm³ at s.t.p]

                                         N₂O₄      ↔        2NO₂  

Initial  moles,                     0.0302            0

mole at equilibrium   0.0302(1-α)   0.0302(2α)

total moles at    equilibrium

              = 0.0302(1-α) + 0.0302(2α) = 0.03763mole

• α = 0.25

Mole

Factors affecting equilibrium

These are

1. Temperature

2. Pressure

3. Catalyst

4. Concentration

The effect of the above factors on equilibrium position for the equilibrium mixture can be explained qualitatively by Le Chatelier’s Principles that states that; ‘ if a system in equilibrium is subjected to a change, processes occur which tend to counteract the change imposed’.

Alternatively, ‘if the concentration of one of the reacting substance is altered, the equilibrium will shift in such a way as to oppose the change in concentration’

Effect of temperature

The effect of temperature on equilibrium depends on whether the reaction is endothermic or exothermic.

(i) For exothermic reactions (∆H⁰ negative) equilibrium position shifts to the left as temperature rise leading to a reduction in equilibrium constants

(ii)   for endothermic reactions (∆H⁰ positive) equilibrium position shift the right as temperature increases leading to increase in the value of equilibrium constants.

Alternatively, the direction of change is given by Vant Hoff’s Law of mobile equilibrium: “if a system is in equilibrium raising the temperature will favor that reaction which is accompanied by absorption of heat, and lowering temperature will favor that reaction which is accompanied by evolution of heat.

NB. It must be emphasized that it is only temperature that can alter the equilibrium positions and values of equilibrium constants among the factors states above whereas other factors alter only the equilibrium positions.

Effect of a catalyst

Catalysts have no effect on the equilibrium constants Kc or Kp because they increase the rate of both forward and backward reaction in an equilibrium equally. However, they increase the rate at which equilibrium is attained.

Effect of concentration on equilibrium mixture

Variations in concentration of the reactant at constant temperature has no effect on the value of equilibrium constants Kp  and Kc. However, if the concentration of one of the reacting substance in a reversible equilibrium is altered, the equilibrium will shift in such away as to oppose the change in concentration.

Effect of pressure changes on equilibrium

1. Pressure has appreciable effects when at least one of the reactant or product in a reversible reaction is a gas because unlike liquids and solids, gases are compressible.
2. The effect of pressure on equilibrium where reactants and/or products are in gaseous form depends on whether there is change in the number of molecules of the gases as the reaction proceeds from left to right.

(i) In general, for gaseous reaction in which there is a change in the number of molecules, increase in pressure favors a reaction which produces fewer molecules or number of moles of the products.

(ii) Pressure has no effect on those gaseous reactions in which there is no change in number of molecules as the reaction shifts from left to the right. e.g.

      H₂(g) + I₂ (g) ↔        2HI(g)

3.   Generally high pressure increases the rate at which equilibrium is attained in gaseous mixture because it increases the rate of collision of the reacting molecules.

4. Pressure has no effect on numerical values of  Kc and Kp at constant temperature although the equilibrium concentration of reactants and product can vary over a wide range.

Example 5

Hydrogen reacts with nitrogen to produce ammonia according the following equation

                3H₂(g)   + N₂(g)     ↔     2NH₃(g)

(a) Write an expression for the equilibrium constant Kc (1 mark),

(b) State, giving reasons, what would happen to the value of the equilibrium constant when

(i) Pressure is increased at constant temperature                                       (3marks)

There will be no effect on the equilibrium constant because only temperature varies the value of the constant.

(ii) argon is added to the reaction mixture at constant pressure           (2marks)

There will be n effect on the equilibrium constant as long as temperature is constant.

(ii) Argon is added to the reaction mixture at constant volume                             (3marks)

This will increase pressure but there will be no change on the value of equilibrium constant of mixture because this value is not altered by pressure.

Watch this

Then this

For revision questions download PDF

Chemical equilibrium

Sponsored by The Science Foundation College +256 753 80 27 09

Compiled by Dr. Bbosa Science