Deflection of an electron in a magnetic field

Deflection of an electron in a magnetic field

Consider an electron entering a uniform magnetic field of flux B, at right angles to its direction of motion with velocity u.

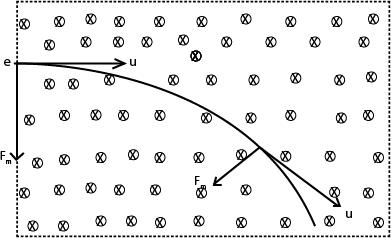
When the electron enters the field, the magnitude of its speed u does not change because the magnetic force is perpendicular to the direction of the electron, But instead its direction changes and the electron moves in a circular arc.

Let r be the radius of the circular arc (path)

Crossed fields

Crossed fields are fields in which a uniform magnetic field and a uniform electric field are perpendicular to each other producing deflections opposite to each other. If the magnetic force and electric force in the crossed fields are of the same magnitude, there is no deflection on charged particles that enter such fields.

The slits S₁ and S₂ confine the particles into a narrow beam as they enter the crossed fields. The only particles that emerge at slit S₃ are those which are undeflected, and therefore they emerge with the same velocity u.

The electric force F_E due to the electric field = eE

The magnetic force F_m due to the magnetic field = Beu

For crossed fields F_E = F_m

eE = Beu

Please Subscribe to promote this website. Subscription is free

Share with a friend

Your comment is valuable

Thank you so much