Ionic equilibrium

Ionization of a weak acid

A weak acid is one that is partially ionized in water. For instance a weak acid HA will ionize in water as follow

HA (aq) + H₂O(l)    ↔        H⁺(aq) + A^–(aq)

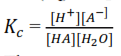
The concentration of H₂O is almost constant such that it can be incorporated in  ti give another constant Ka

The greater the extent of dissociation, the greater is [H⁺] and [A-] in solution; the greater the Ka, and the stronger is the acid.

Alternatively, the strength of the acid is expressed in terms of pH.

The ‘p’ in pH comes from the German word ‘potenz’ meaning power and ‘H’ from [H⁺]. The pH of solution is the negative logarithm to base ten of the molar concentration of hydrogen ions.

i.e., pH = -log₁₀ [H⁺]

Example 1

The pH of 0.1M ethanoic (acetic) acid, CH₃COOH, is 3.40 at 25⁰C.What is the dissociation constant of ethanoic acid at this temperature?

solution

Equation

CH₃COOH (aq)     ↔      CH₃COO^–(aq) + H⁺(aq)

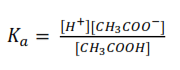
Since the concentration of H+ ions form water is much smaller that the concentration of those from acid; [H+] ≈ [CH₃COO^–] = antilog-3.4

                                  = 4.0 x 10^-4moldm^-3

and [CH₃COOH] = 0.01 – [H⁺] ≈ 0.01

Example 2

RCO₂H  is a weak acid

(a) Write the equation for the ionization of the weak acid RCOOH in water (1 mark)

ans: RCOOH (aq)    ↔      RCOO^–(aq) + H⁺(aq)

(b) Write the expression for the ionization constant Ka, for the acid.

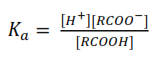
(c) Calculate the hydrogen ion concentration of 0.25 M solution for the acid (  = 1.8 x 10^-5) (4 marks)

Solution

Let [H⁺] = x

Also, [H⁺] = [RCOO^–] = x

[RCOOH] = [0.25 – x) ≈ 0.25 moldm^-3, since the concentration of H+ is very small.

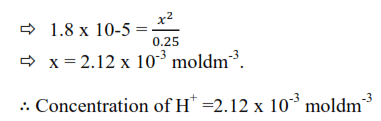
Ionization of weak base

A base is a substance that abstracts a proton from water or dissociates in water to produce hydroxyl ion. Like weak acid, weak base are only partially dissociated in water.

B(aq) + H₂O(l)    ↔      BH⁺(aq)+OH^–(aq)

The concentration of H₂O is almost constant such that it can be incorporated in  to give another constant Kb

Like Ka, Kb is a function of temperature, and the higher the Kb the stronger the base.

Example 3

(a) At 250C ammonia has a base ionization constant  = 1.8 x10^-5moldm³.

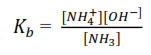
 (b) Calculate the concentration of [^–OH] in 0.1M ammonia solution at 25⁰C. state any assumption

Log [OH^–] be x

Assumption: OH^– ions from ionization of water are negligible compared to those from ionization of ammonia

[OH^–] = [NH₄⁺] = x

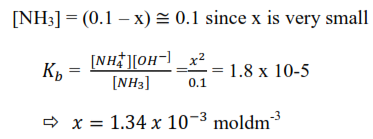
Dissociation of water

Water ionizes as follows

H₂O(l)      ↔       H⁺(aq) + OH^–(aq)

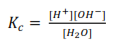
The concentration of  H₂O is constant and is incorporated in the value of Kc  to give a new constant, Kw. .

Kw = [H⁺][OH^–]

 is ionic product for water, at 25⁰C  pure water has Kw = 1 x 10 ^-14 mol²dm^-6.

Application of

It is used to determine the pH of bases

Example 4

Calculate the pH of 0.1M NaOH solution

Solution

Sodium hydroxide dissociate in water as follows

NaOH(aq) → Na⁺(aq) +OH^–(aq)

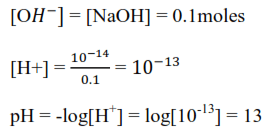
Watch the video

Buffers

These are solutions that resist changes in pH on addition of small amounts of either the acid or base.

Buffers are usually made of either a mixture of a weak acid and its salt with strong base (e.g. CH₃COOH + CH₃COO^–Na⁺) or a mixture of a weak base and its salt with a strong acid (e.g. NH₃ + NH₄Cl)

Mechanism of buffers

Consider a hypothetical weak acid, HA, in a solution with it salt MA. In this solution, HA, will be very slightly dissociated whilst MA is fully dissociated into ions;

HA (aq)  ↔       H⁺(aq) + A^–(aq)

MA(aq) → M⁺(aq) + A^–(aq)

Hence the mixture contains a relatively high concentration of un-ionized HA (acid) and relatively high concentration of A^– (base)

If an acid is added to this system, the H⁺ ions in the acid will combine with A^—ions to form HA thus removing nearly all the added H+ ions and keeping the pH relatively unchanged.

H⁺(aq) + A^–(aq) → HA(aq)

When an alkali is added to a system, the added ^–OH ions combine with the acid to produce water

HA(aq) + ^–OH(aq) → H₂O(l) + A^–(aq)

By having the reserves of HA and A- in buffer changes resulting from the addition of acid or alkali are minimized.

Calculating the pH of the buffer solution

In a buffer composed of a weak acid HA and its salt MA

HA    ↔       H⁺+ A^– and MA →M⁺+ A^–

The expression for dissociation constant of HA is written as

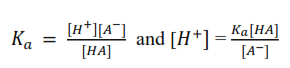
In the buffer mixture [HA] ≈ [acid] since the acid will be very slightly dissociated in presence of its salt and [ A^–] ≈  [salt] since the salt is fully dissociated

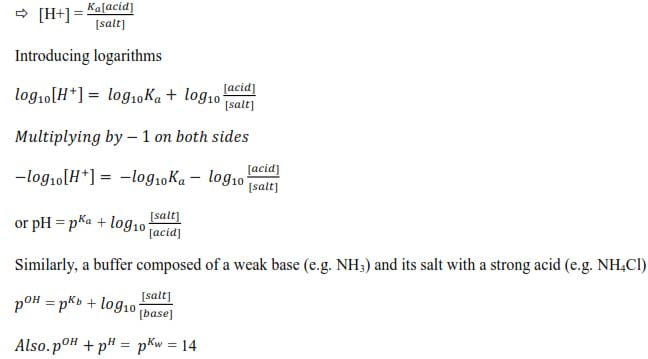
Example 5

Calculate the pH of the buffer made by adding 3.28g of sodium ethanoate to 1dm³ of 0.01M Methanoic acid. Ka(CH₃COOH =1.75 x 10^-5moldm^-3)

Solution

Hydrolysis of salts

 

It is the reaction of a salt with water to produce either acid or alkaline solution. The type of hydrolysis depends on the nature of salt.

(i) A salt formed by reacting a weak acid and a strong base hydrolyzes to give an alkaline solution. for example, sodium ethanoate is highly dissociated while water is very slightly ionized. The reaction occurs in solution as follows:

CH₃COO^–Na⁺ →CH₃COO^– + Na⁺

then,

CH₃COO^–(aq) + H₂O ↔          CH₃COOH(aq) + ^–OH(aq)

Expression of K_h in terms of Kw and Ka

Multiplying [H⁺] through the numerator and denominator give;

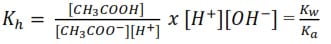
(ii) A salt of a weak base and a strong acid hydrolyzes in water to give acid solution

e.g. NH4Cl dissociate in water as follows

NH₄⁺ + H₂O      ↔        NH₃ + H₃O⁺

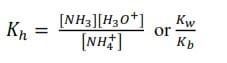
Example 6

Sodium benzoate undergoes hydrolysis when dissolved in water

(a) Write an equation for hydrolysis of sodium benzoate

C₆H₅COO^– (aq) + H₂O (l)      ↔      C₆H₅COOH (aq) + OH^–(aq)

(b) Write an expression for the hydrolysis constant K_h.

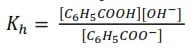
(c) The hydrolysis constant of sodium benzoate is 1.6 x 10^-5moll^-1.

(i) Calculate the concentration of the hydroxide ions in a 0.10M sodium benzoate  at 25⁰C. (Kw = 1 x10^-14 mol²dm^-6)      (4marks)

Solution

Let the concentration of OH^– ions be x

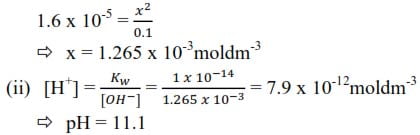
(iii) State any assumption made in c(i) above

Hydrogen ions or hydroxyl ions from ionization of water are negligible

 

The solubility of sparingly soluble ionic solids in water

https://youtu.be/WtJzL9ZXiR0

 

When a sparingly soluble salt such as silver chloride or barium sulphate, is added to water, a little dissolves and produces ions in solution. Equilibrium is established between the ions and the solid salt when the rate at which ions leave the crystal frame work of the solid is equal to the rate at which they are deposited again. Since the solubility is very small, the ions present in the liquid are few in number and are so far apart that they are free from mutual interference. We can therefore say that in the very dilute saturated solution the solution is completely dissociated.

With a solution of a sparingly soluble electrolyte AxBy in contact with the solid the dissociation can be expressed as follows

AxBy + aq     ↔       xA^y+ + yB^x-

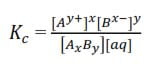
Since the salt is only slightly dissociated in water, the [AxBy] and [aq] are constant

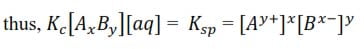
The constant Ksp/Ks  is the solubility product of the electrolyte, AxBy.

The solubility product of a sparingly soluble electrolyte is the product of the concentration of ions in a saturated solution raised to corresponding Stoichiometric ration in the salt. The higher the Ksp  is the higher the solubility of the salt.

Example 7

The solubility of silver chloride at 18⁰C is 1.46 x 10^-3gdm^-3. What is the solubility product (Ag =108, Cl = 35.5)

Solution

Note that in the calculation of solubility products the concentrations are expressed in moledm^-3 or moll^-1

Mass of 1mole of AgCl = 108 + 35.5 = 143.5g

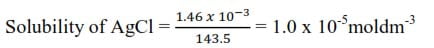
Since one ‘molecule’ of silver chloride furnishes on dissociation one Ag⁺ ion and one Cl^– ion, and since the dissolved silver chloride is completely dissociated in ions

 = [Ag⁺][Cl^–] = (1 x 10^-5)(1 x 10^-5)   = 1 x 10^-10mol²dm^-6

Example 8

The solubility of calcium hydroxide in water at 20⁰C is 2.78gdm^-3. What is the solubility product? (Ca = 40, O = 16, H = 1)

Solution

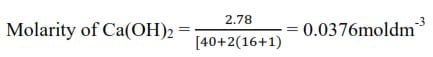
[Ca²⁺] = 0.0376moldm^-3

[OH^–) = 2 x 0.0376 = 0.0752moldm^-3

 = [Ca²⁺][OH^–]² = 0.0376 x (0.0752)²

       = 2.13 x 10^-4mol³dm^-9

 Limitation to the solubility product concept

1. Salts like potassium nitrate of relatively high solubility, do not possess solubility products because the law of mass action does not hold in their case. The solubility product concept is only valid for saturated solution in which the total concentration of ions is no more than about 0.01M
2. The solubility product constant, like all other equilibrium constants change with temperature; consequently, the temperature at which solubility product is measured should always be specified unless it relates to the standard temperature of 298K or 25⁰C.

Application of solubility product concept

(a) The common ion effect

This is the reduction in the solubility of a sparingly soluble salt in a solution in which it has a common ion.

Although the solubility product of a particular salt is constant at a constant temperature, the concentrations of the individual ions may vary over a very wide range.

When a saturated solution is obtained by dissolving the pure salt in water the concentration of the ions produced are in the ratio determined by the stoichiometry of the compound.

E.g. concentration of Ag⁺ and CrO₄^2- ions in pure saturated silver chromate solution must be in ration 2:1. However, when a saturated solution is obtained by mixing two solutions containing a common ion (such as Ag₂CrO₄ and AgNO₃) there may be a big difference in the concentration of ions of any sparingly soluble electrolyte. In this case, the solubility product is used to determine the concentration of the ions in solution.

Example 9

Calculate the solubility of BaSO₄ in

(i) Water?

(ii) in 0.1M sodium sulphate solution?

    (Ksp = 1 x 10^-10mol²dm^-6)

Solution

(i) BaSO₄ dissociate as follows

BaSO₄(s)   ↔      Ba²⁺(aq) + SO₄^2-(aq)

Let the solubility be x

[Ba²⁺] = [SO₄^2-] = x

 Ksp = [Ba²⁺][SO₄^2-] = x² = 1 x 10^-10

  x = 1 x 10^-5moldm^-3.

(ii)  Solubility of BaSO₄ in water = 1 x 10^-5moldm^-3

Let the solubility of BaSO₄ in 0.1M Na₂SO₄ be y

Na₂SO₄(s) dissociates as follows

Na₂SO₄ (aq) → 2Na⁺(aq) + SO₄^2-(aq)

[Ba²⁺] =  y

[SO₄^2-] = (0.1 + y)

= y(0.1+y) = 1 x 10^-10

y is very small that (0.1+y) ≈  0.1

thus 0.1y = 1×10^-10

y = 1 x 10^-9moldm^-3

 The solubility of BaSO₄ in 0.1M Na₂SO₄

                                                   = 1 x 10^-5moldm^-3

This example illustrate that BaSO4 is more soluble in water than in NaSO4 solution that contains a common ion (i.e. SO₄^2-)

 (b) Prediction of Precipitation

The solubility product is used to predict the maximum concentration of ions in solution at a given temperature and hence whether or not precipitation will occur.

Suppose we mix 0.001M CaCl₂ solution (which contains 0.001M Ca²⁺ ions) with equal volume of 0.001M Na₂SO₄ (i.e. 0.001M SO₄^2- ions) solution at 25⁰C. Will a precipitate of CaSO₄ formed? ( Ksp  CaSO4 = 2 x 10^-5mol²dm^-6)

Immediately after mixing equal volumes of the two ions and before any precipitation

[Ca²⁺] = [SO₄^2-] = 5 x 10^-4M

(i.e. the concentration of each ion is halved since each solution is diluted by mixing with the other). Hence the ionic product for CaSO₄ immediately after mixing

[Ca²⁺][SO₄^2-]    = 5 x 10^-4 x 5 x 10^-4  

                        = 2.5 x 10^-7mol²dm^-6

This ionic product is less than the value of Ksp  for CaSO₄ and so no precipitation occurs.

Let ionic now suppose that we mix equal volumes of 0.01M solution of each. Immediately after mixing

[Ca²⁺] = [SO₄^2-] = 5 x 10^-3M and ionic product

[Ca²⁺][SO₄^2-]    = 5 x 10^-3 x 5 x 10^-3  

                        = 2.5 x 10^-5mol²dm^-6

In this case, the ionic product is greater than the solubility product and therefore precipitation of CaSO₄ occurs.   The concentration of aqueous Ca²⁺ and SO₄^2- ions are lowered by the reaction.

Ca²⁺ (aq) + SO₄^2-(aq) → CaSO₄ (s)

Coral reef, stalagmite and stalactites are result of slow precipitation of CaCO₃ from water when concentration of Ca²⁺ and CO₃^2- exceed the  Ksp  of CaCO₃.

(c) Selective precipitation

This is used to separate salts with different solubility,. e.g. Ca²⁺, Mg²⁺ and Ba²⁺ can be separated by adding K₂Cr₂O₄(aq), which precipitate out BaCrO₄ (which is the least soluble) and removed by filtration. The remaining solution that contain Mg²⁺ and Ca²⁺ is then separated by adding Na₂SO₄ that precipitate out CaSO₄ (CaSO₄ in less soluble than MgSO₄) leaving Mg²⁺ in solution

Note that the order in which reagents are added is important. If we had added Na₂SO₄ solution before adding K₂CrO₄ solution a mixture of BaSO₄ and CaSO₄ would have been precipitated.

On the other hand, if Na₂CO₃ solution had been added to the mixture of the three cations; MgCO₃, CaCO₃ and BaCO₃ would all have been precipitated. Thus, both the precipitating reagent and the order of addition must be selected with great care.

(d) Use of potassium chromate (VI) in silver nitrate titration

When silver nitrate solution is titrated with sodium chloride solution containing a little potassium chromate (VI) only silver chloride is precipitated as long as there are any chloride ion in solution.

Only when all chloride ions have reacted doe a red precipitate of silver chromate (VI) appear. This is explained by the solubility products of the two silver salts; i.e. (Ag⁺)(Cl^–) = 1 x 10^-10mol²dm^-6 while (Ag⁺)₂(CrO₄^2-) = 2.5x 10^-12mol³dm^-9. Suppose the concentration of Cl^– and  CrO₄^2- ions in the liquid are both 0.1M. Then

[Ag⁺] needed to precipitate silver chloride

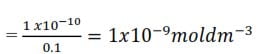
[Ag⁺] needed to precipitate silver chromate

Thus even if the concentration of the Cl^– ions and CrO₄^2- ions in the liquid are equal, it is easier by adding Ag⁺ ions to reach the solubility product of the chloride than that of the chromate (VI) in spite of the lower solubility product of the latter. In practice [Cl^–] is much larger than [CrO₄^2-]. Hence silver chloride I precipitated even more readily.

Indicators

https://youtu.be/b4iUwRCQLe8

 

Acid-base indicators are substances which change color according to the hydrogen ions concentration of the liquid in which they are placed. They are either weak acids or weak bases, and are therefore slightly dissociated when dissolved in water. The color of the indicator depends on the color of the un-dissociated molecules and the color of the ions produced. Taking methyl orange as an example, dissociation occurs as follows:

More precisely

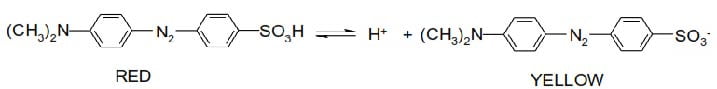
When a drop of methyl orange is added to water, the resultant color is orange. if now an acid is added, the hydrogen ions of the acid drive back the ionization of methyl orange, very few Me^– ion remain, and the indicator becomes pink.

Alternatively, the addition of a base provides a large concentration of hydroxyl ions which combine with the H⁺ of the indicator to form water.

More of the indicator ionizes and a large concentration of Me^– ions are produced, giving a yellow color. similarly, litmus has red HA and blue A^– ions.

Neutrality/ Endpoint of indicator

The aim of any titration is to determine the volume of two solutions that just react with each other. Thus, the endpoint which is the point at which the titration is stopped must coincide with the equivalence point for the two reacting solutions.

In order to achieve this, the indicator should change color sharply at an equivalent point on the addition of a single drop of either acid or alkali. At the exact endpoint of the titration; the color of the indicator will be midway between the acid color HIn and the color of In^–. If the dissociation constant of the indicator

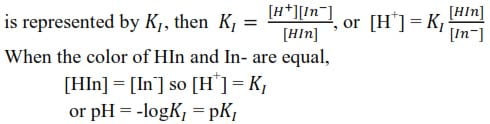
Range of an indicator

Every indicator has a definite range of pH over which it changes color given by

The colors and pH ranges of some common indicators are given in the table below:

Indicator	pH range	acid	alkali
Thymol blue	1.2-2.8	red	yellow
Methyl orange	2.9-4.6	pink	yellow
Congo red	3.0-5.0	blue
Methyl red	4.2-6.3	pink	yellow
Litmus	5.0-8.0	red	blue
Phenolphthalein	7.4-9.0	colorless	red

PH changes during titration

During a titration, there is a change in pH as alkali is added to acid or vice versa. At the equivalent point, the pH must change sharply by several units for it to be identifiable using an indicator.

The change in pH during the course of a titration depends largely upon the strength of the acid and alkali used.

The figure shows the effect on pH value of adding to 50cm³ molar HCl (strong acid) increasing quantities of molar solution of NaOH  and secondary, a solution of NH₃ (a weak base)

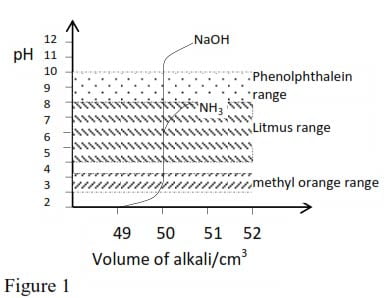
Note that, with NaOH addition of a very small volume of the base near the end point provides a very large change in the hydrogen ions concentration almost completely covering the pH ranges of methyl orange, litmus and phenolphthalein; In practice any of these indicator may be used during a titration of a strong acid with a strong base.

With ammonia solution adding a small amount of base near end point produces a small change in hydrogen ion concentration, and the end point is less sharp, no matter what indicator is used; although methyl orange provides the best choice.

The effect on pH value of adding to 10 cm³ of molar ethanoic acid (weak acid) increasing quantities of first molar NaOH solution (strong base and secondly, molar ammonia (weak base) is illustrated in figure below

In the first case a less sharp endpoint that with a strong acid and strong base is again obtained with phenolphthalein as the best indicator for this titration.

When the acid and the base are both weak, the endpoint is so indefinite that in practice a weak acid and weak base are never titrated against each other.

Choice of indicator

The true endpoint of neutralization in any titration occurs when the amount of acid and base added together are chemically equivalent to each other. The solution may not have a pH= 7 (i.e. neutral) equal to that of water at this point.

With strong acids and strong base the final pH is about 7. In other cases hydrolysis of salt takes place, producing a pH greater or less than 7. Thus according to figure 1, the pH is about 5 for 0.5M NH4Cl solution, and from figure 2 about 9 for a 0.5M solution of sodium ethanoate (CH₃COONa).

For a strong acid and a strong base the theoretically correct indicator is litmus, but in practice both methyl orange and phenolphthalein can be used. Similarly, methyl orange (or more accurately methyl red) is the correct indicator for titrating aqueous ammonia and hydrochloric acid, and phenolphthalein for sodium hydroxide and ethanoic acid. The general rules for indicators can be summarized as follows:

Strong acid and strong base – any indicator

Strong acid and weak base – methyl orange

Weak acid and strong base – phenolphthalein

Weak acid and weak base are not titrated.