
Heat A-level physics revision questions with answers

- (a) (i) State any three properties of ultraviolet radiation.(03marks)
- Produces ionization
- Produces fluorescence
- Affects photographic films
- Produces photoelectric effect
- Absorbed by glass
- Can be polarized
- Promotes chemical reactions
(ii) What is a black body? (01mark)
A black body is one that absorbs all radiations incident on it without reflecting or transmitting any.
(b) A cylindrical metal rod with a well- insulated curved surface has one end blackened and then exposed to thermal radiation from a body at a temperature 500K. If the equilibrium temperature of the blackened end is 400K and the length of the rod is 10cm, calculate the temperature of the other end. [Thermal conductivity of the metal = 500Wm-1K-1] (04marks)

(c) (i) Describe Electrical method of determining the specific heat capacity of a good conducting solid. (06marks)

- Two holes are drilled into the specimen solid of mass m.
- A thermometer is inserted in one of the holes and an electric heater into the other hole. The holes are then filled with a good conducting fluid, e.g. oil to ensure thermal contact.
- The apparatus is insulated and initial temperature θ0 is recorded.
- The heater is switched on at the same time a stop clock is started.
- The steady values of ammeter reading, I and voltmeter reading, V are recorded.
- After considerable temperature rise, the heater is switched off and stop clock stopped.
- The highest temperature θ1 recorded and time t taken noted.
- The specific heat capacity, c, of the conducting solid is calculated from

(ii) Give two reasons why the value obtained using the method in (c)(i) may not be accurate. (02marks)
- some heat is lost to the surrounding through the insulator
- some heat is absorbed by the thermometer and heater
- the solid expands during heating and so external work is done against atmospheric pressure.
(d) Explain why cloudy nights are warmer than cloudless ones.
During day, radiation is absorbed from the sun by earth. At night, the earth radiated heat into the atmosphere.
On a cloudless night, the radiated heat is lost. On cloudy night, the clouds form blanketing layer which reflects back the heat to the earth and warmth feeling.
- (a)(i) What is meant by a reversible process? (02marks)
A reversible process is a process that can proceed in a reverse direction by very small change in conditions making it take place through exactly same steps.
(ii) Distinguish between a saturated vapour and unsaturated vapour. (02marks)
A saturated vapour is one that is a dynamic equilibrium with its own liquid while unsaturated vapour is not in dynamic equilibrium with its own liquid.
(iii) Explain why evaporation causes cooling(03marks)
When a liquid vaporizes, the most energetic molecules escape from the surface leaving less energetic molecules in the liquid. Since temperature is directly proportional to kinetic energy of the molecules, the liquid cools.
(b) Describe an experiment to determine the temperature dependence of saturated vapour pressure of water. (07marks)

- The pressure of the air in R is shown by the mercury manometer; if its height is h, the pressure in mm mercury is P = H-h, where H is the barometer height.
- The tap is opened and the pressure above water varied using the pump to a suitable value.
- The tap is closed and water in the flask in heated until it boil.
- The temperature θ and difference in mercury levels, h, are noted and recorded.
- The saturated vapour pressure, P = (H± h) is calculated
- The procedure is repeated other values of θ and h
- A graph of P versus θ is plotted and it shows that saturated vapour pressure, P, increases with temperature, θ.
(c) (i) State Dalton’s law of partial pressures. (02marks)
Dalton’s law states that the total pressure of a mixture of gases that to not react chemically is equal to the sum of the partial pressure of the components of a gas.
(ii) A sealed container has liquid water, water vapour and air all at 270C. The total pressure inside the container is 69cmHg. When the temperature is raised to 850C, the total pressure changes to 96cmHg. If the saturated vapour pressure of water at 270C is 5cmHg and water vapour remains saturated, calculate the saturated vapour pressure of water at 850C. (05marks)
T1 = 27 + 273 = 300K
T2 = 85 + 273 = 358K
Partial pressure at T1; P1 = 69-45 = 64cmHg
Partial pressure at T2, P2 = (96 –P) cmHg
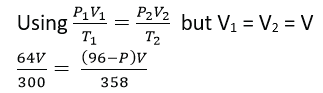
P = 19.63cmHg
- (a) Define the following:
(i) Thermal conductivity. (01marks)
Thermal conductivity s the rate of heat flow per unit cross section area per unit temperature gradient
(ii) Specific latent heat of vaporization. (01mark)
Specific latent heat of vaporization is the amount of heat energy required to change 1kg of a liquid to vapour at constant temperature.
(b) A boiler with a base made of rod steel 15cm thick, rests on a hot stove. The area of the bottom of the boiler is 1.5 x 103 cm2. The water inside the boiler is at 1000C. If 750g of water is evaporated every 5 minutes, find the temperature of the surface of the boiler in contact with the stove. [Thermal conductivity of steel = 50.2Wm-1K-1, specific latent heat of vaporization of water = 2.26 x 106Jkg-1]
Solution
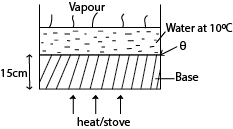
Rate of heat flow through the boiler = Rate of heat supplied to vaporize water
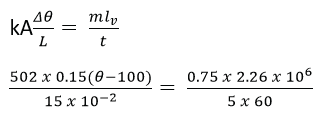
θ = 21280C
(c) Hot water in a metal tank is kept constant at 650C by an immersion heater in the water. The tank has lagging all around it of thickness 20mm and thermal conductivity0.04Wm-1K-1 and its surface area is 0.5m2. The heat lost per second by the lagging is 0.8W per degree excess above the surroundings. Calculate the power of immersion heater if the temperature of the surroundings is 150C. (05marks)
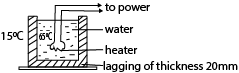
K = 0.04Wm-1K-1, A = 0.5m2, L = 20 x 10-3m
Let θ be the temperature of the lagging
Excess temperature = (θ – 15)
Heat lost per second = 0.8(θ – 15)

θ = 42.80C
Power of heater = 0.8(42.8 – 15) = 22W
(d)(i) Define thermometric property (01mark)
Thermometric property is a physical measurable property that varies linearly and continuously with temperature and is constant at constant temperature.
(ii) Define how a liquid-in-glass thermometer can be used to measure temperature in degrees Celsius. (04marks)
- A bulb is inserted in pure ice-water mixture.
- After some time, the constant length, l0 of mercury thread is recorded.
- The bulb is inserted in steam and constant length, l100 of mercury thread is recorded.
- When lθ is the length of mercury thread inserted in an unknown enclosure of temperature, θ0, then
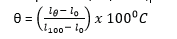
(iii) A thermometer is constructed with a liquid which expands according to relation. Vt =V0(1 + αt + βt2). Where Vt is the volume at t0C and V0 is the volume at 00C on the scale of the gas thermometer and α and β are constants.
Given that α = 1000β, what will the liquid thermometer read when the gas thermometer reads 500C.
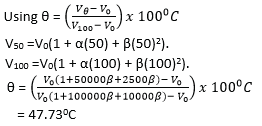
- (a) Define the following quantities:
(i) Thermometric property (01mark)
Thermometric property is a physical measurable property that varies linearly and continuously with temperature and is constant at constant temperature.
(ii) Specific heat capacity (01mark)
Specific heat capacity is the amount of heat requires to raise the temperature of 1kg mass of a substance by 1K or 10C
(b) (i) state two examples of commonly used thermometric properties. (01mark)
- e.m.f of thermocouple
- pressure of a gas
- volume of mercury in glass
(ii) Describe briefly how to determine the lower and upper fixed points for an uncalibrated liquid-in-glass thermometer (04marks)
- the bulb of the thermometer is immersed in pure ice-water mixture; the level of liquid column falls to a constant length. The level of the liquid column is marked and is the lower fixed point.
- the bulb of the thermometer is then immersed in steam from pure water; the level of liquid column rises to a constant length. The level of the liquid column is marked and is the upper fixed point.
(c) (i) Describe with the aid of a diagram, an experiment to determine the specific heat capacity of a liquid using the continuous flow method. (07marks)

- A liquid is allowed to flow at constant rate
- Power is switched on and the liquid is heated until temperatures registered by T1 and T2 are steady and the values θ1 and θ2 respectively are recorded.
- The p.d V and current I are recorded from the voltmeter and ammeter respectively
- The mass, m of a liquid collected in time t is recorded
- At steady state; VIt = mc(θ2 – θ1) + h ………….. (i)
where h is heat lost to the surrounding
- The rate of flow is changed and the voltage and current are adjusted until the steady readings of T1 and T2 are θ1 and θ2 respectively
- If m1, V1 and I1 are the values mass of liquid collected in time t, voltmeter and ammeter readings respectively, then
V1I1t = m1c(θ2 – θ1) + h ………….. (ii)
- Subtracting (ii) from (i)
![]()
(ii) State two advantages of the continuous flow method over the method of mixtures. (01mark)
- No cooling correction is required
- Heat capacity of the apparatus is not requires
- Temperature measured at leisure when steady
- Resistance of the heater not required
(iii) State two disadvantages of the method in (c)(i) (01mark)
- larger volumes of liquid required
- not suitable for volatile liquids.
(d) The brake lining of the wheel of a car of mass 800kg have total mass of 4.8kg and are made of a material of specific heat capacity 1200Jkg-1K-1. If the car is at 15ms-1 and is brought to rest by applying the brakes, calculate the maximum possible temperature rise of the brake lining. (04marks)
Mechanical energy = heat absorbed by the lining

- (a) (i) What is meant by conduction of heat? (01mark)
Conduction of heat is a process of heat transfer by which heat floe from a hotter region of a substance to the cold regions without the bulk movement of a substance as a whole.
(ii) Explain why mercury conducts heat better than water. (03marks)
Mercury has free electrons capable of transferring energy without any part of mercury moving. Mercury atoms are closer allowing conduction of atomic vibrations while in water there is no free electrons and atoms are farther apart.
(iii) Explain the occurrence of land and sea breezes. (06marks)
During day, the land is heated to a high temperature than the sea. Hot air expands and rises from land. A stream of cool air from the sea blows towards the land to replace the uprising air, hence sea breeze occurs.
At night the land cools faster because it is no longer heated by the sun. the sea retains the warmth because it is heated deeply. Warm less dense air rises from the sea surface and air from land blows to replace it leading to land breeze.
(b) A copper sphere of radius 7cm and density 900kgm-3, is heated to a temperature of 1270C and then transferred to an evacuated enclosure whose walls are at a temperature of 270C. Calculate
(i) net rate of loss of heat by the copper sphere
![]()
(ii) temperature of copper sphere after 5minutes

(c) Explain why heating system based on the circulation of steam are more efficient than those based on circulation of boiling water. (02marks)
A given mass of steam gives out more energy that an equal amount of water because of the specific latent heat.
- (a) (i) what is meant by a black body? (02marks)
A black body is a body that absorbs all radiations incident on it and transmits or reflects none
(ii) Give two examples of a black body. (01mark)
- The sun
- Star
- Black hole (remnants of a star after it has used up all its energy]
- An almost enclosed blackened surface with hole/furnace with small hole
(b) With aid of graphs describe how radiation emitted by a black body varies with wavelength for two temperatures.
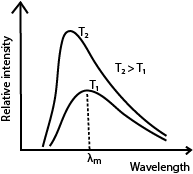
Intensity increases as temperature increases. The increase is more rapid for shorter wave length. For each temperature T, the distribution curve has a wavelength (λm) corresponding to maximum intensity. λm decreases as temperature increases.
(c) (i) Define thermal conductivity. (01mark)
Thermal conductivity is the rate of heat transfer per unit cross section area per unit temperature gradient.
(ii) Describe an experiment to determine thermal conductivity of glass. (07marks)

- Glass s cut in form of a thin disc of cross section area, A and thickness, x.
- The disc is sandwiched between a steam chest and brass slab of mass, m and specific heat capacity, c.
- Steam is passed through the chest until the thermometers register steady temperatures, θ1 and θ2.
![]()
- The glass disc is removed and brass slab is heated directly by steam chest, until its temperature is about 100C above θ1.
- Steam chest is removes and the top of the glass slab is covered by the glass disc.
- The temperature of the slab is recorded at suitable time interval until its temperature is about 100C below θ1.
- A graph of temperature against time is plotted and its slope s determined at θ1
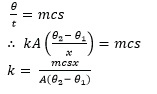
(d) Radiation from the sun falls normally on a blackened roof measuring 20m x 50m. If half of the solar energy is lost in passing through the earth’s atmosphere, calculate the energy incident on the roof per minute. [Temperature of the sun’s surface = 6000K; radius of the sun = 7.5 x 108m, distance of the sun from the earth = 1.5 x 1011m]

- (a) (i) State the thermometric property used in a constant-volume gas thermometer (01mark)
pressure
(ii) Give two characteristic of a good thermometric property, (02marks)
- should vary linearly with change in in temperature
- Should vary continuously with temperature
- Should be sensitive to temperature changes
- Should be measurable
- Should vary over a wide range of temperature.
(b) (i) Describe the steps taken to set up a Celsius scale of temperature for a mercury-in glass thermometer. (04marks)
- A bulb is inserted in pure ice-water mixture.
- After some time, the constant length, l0 of mercury thread is recorded.
- The bulb is inserted in steam and constant length, l100 of mercury thread is recorded.
- When lθ is the length of mercury thread inserted in an unknown enclosure of temperature, θ0, then
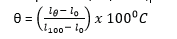
(ii) State four disadvantages of a mercury in glass thermometer. (04marks)
- it is not very sensitive
- it cannot measure rapidly changing temperature
- it is delicate, i.e. it breaks easily
(c) Describe with the aid of a diagram the operation of an optical pyrometer (06marks)

- the filament is focused on the eye piece and the objective lens focuses the object so that the image of the object lies in the same plane as the filament
- Light from the hot object and the filament is passed through the red filter and viewed by the eyepiece.
- Current is adjusted by the rheostat R until the filament and the object are equally bright.
- The temperature of the hot body is then read from the calibrated ammeter, A.
(d) When oxygen is withdrawn from a tank of volume 50L, the reading of pressured gauge attached to the tank drops from 4.4 x 105 Pa to 7.8 x 105Pa. If the temperature of gas remaining in the tank falls from 300C to 100C, calculate the mass of oxygen withdrawn.
- (a)(i) What is meant by boiling point? (01marks)
The boiling point of a liquid is the temperature at which its saturated vapour pressure equals the external pressure.
(ii) Explain why boiling point of a liquid increases with increase in the external pressure. (05marks)
When the liquid boils its saturated vapour pressure = external pressure and saturated vapour pressure increases with increasing temperature.
When external pressure is raised, a liquid will boil at higher saturated pressure which occurs at high temperature.
(b) Explain how the pressure of a fixed mass of a gas can be increased at
(i) Constant temperature (03marks)
By reducing the volume occupied by a gas, the molecules take less time to move between the walls of the container as the distance is reduced. The number of collisions per unit area increases hence pressure increases at constant temperature.
(ii) Constant volume (03marks)
By heating the gas, the molecules gain more kinetic energy. The molecules will bombard the walls many times per unit time per unit area. The total rate of change of momentum will increase hence pressure will increase
(c) Sketch a pressure versus volume curve for a real gas undergoing compression (03 marks)
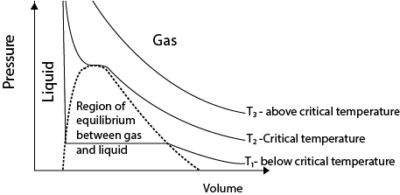
- Above the critical temperature, a real gas behaves ideally.
- Below the critical temperature the turns into a liquid on compression as shown.
- A liquid is not compressible that is why pressure increases very rapidly with a small decrease in volume.
(d) The cylinder of an exhaust pump has a volume of 5cm3. If it is connected through a valve to a flask of volume 225 cm3 containing air at a pressure of 75cmHg, calculate the pressure of air in the flask after two strokes of the pump, assuming that the temperature of the air remain constant.
First stroke
P1V1 = P2V2 but V2 = 225 + 25 = 250cm2
75 x 225 = P2 x 250
P2 = 674cmHg
Second stroke
P2V2 = P3V3
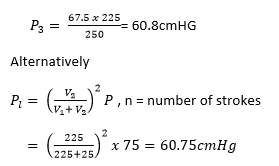
- (a) (i) Define thermal conductivity. (01mark)
Thermal conductivity is the rate of heat flow per unit cross sectional area per unit temperature gradient.
(ii) Explain the mechanism of heat transfer by convention. (03marks)
When a fluid is heated from underneath, it expands and becomes less dense than fluid above. The warm less dense fluid rises to the top and the cool more dense fluid from above moves downwards to take place. This process continues and circulating current of the fluid is established until the whole fluid is heated up.
(b) (i) State Newton’s law of cooling (01mark)
It state that the rate of loss of heat is proportional to the excess temperature between the body and the surroundings under forced convections or steady draught.
(ii) Describe briefly an experiment to verify Newton’s law of cooling. (05marks)
Hot water in a calorimeter is placed near an open window. The temperature of the water is recorded at suitable time intervals. A graph of temperature against time is plotted. Slope of the graph is obtained at temperature θ1. More values of the slope are obtained at different temperatures, θ2, θ3, θ4 ………………
For each temperature, excess temperature, (θ -θR) is calculated, where θR is the room temperature.
A graph of slopes against excess temperature is plotted.
A straight line graph through the origin verifies Newton’s law.
(c) A wall is constructed using two types of bricks. The temperatures of the inner and outer surface of the wall are 290C and 210C respectively. The value of thermal conductivity for the inner brick is 0.4Wm-1K-1 and that of the outer brick is 0.8Wm-1K-1.
(i) Explain why in a steady state the rate of thermal energy transfer is the same in both layers. (02marks)
No heat is lost to the surrounding as it flows through the inner and outer surfaces. The temperature gradient across the composite wall is constant.
(ii) If each layer is 12 cm thick, find the temperature at the interface between the layers. (04mrks)
(d) Explain the greenhouse effect and how it leads to rise of the earth temperature. (04marks)
The short wavelength radiation from the sun penetrates the atmosphere and is absorbed by the earth’s surface. This absorbed energy warms the earth which then re-radiates long wavelength radiations e.g. infrared radiation. Some of this radiated energy absorbed (trapped) by the atmosphere. This leads to increased temperature on the earth with time referred to as global warming.
- (a) (i) Define specific latent het of fusion (01mark)
Specific latent het of fusion is the amount of heat required to change 1kg mass of a substance from solid to liquid without change of temperature.
(ii) State effect of impurities on melting point (01mark)
Impurities lower the melting point.
(b) Explain why there is no change in temperature when a substance is melting (04marks)
Supply of heat to a melting solid reduces the forces of attraction between the molecules and increases the separation between them. This increases the potential energy (P.E) between the molecules while keeping kinetic energy (K.E) of the molecules the same. Further increase in separation between the molecules causes the regular pattern to collapse as the solid changes to liquid. Until this process is complete, the temperature does not change.
(c) With the aid of a labelled diagram, describe the continuous flow method of measuring the specific heat capacity of a liquid. (06marks)

- A liquid is allowed to flow at constant rate
- Power is switched on and the liquid is heated until temperatures registered by T1 and T2 are steady and the values θ1 and θ2 respectively are recorded.
- The p.d V and current I are recorded from the voltmeter and ammeter respectively
- The mass, m of a liquid collected in time t is recorded
- At steady state; VIt = mc(θ2 – θ1) + h ………….. (i)
where h is heat lost to the surrounding
- The rate of flow is changed and the voltage and current are adjusted until the steady readings of T1 and T2 are θ1 and θ2 respectively
- If m1, V1 and I1 are the values mass of liquid collected in time t, voltmeter and ammeter readings respectively, then
V1I1t = m1c(θ2 – θ1) + h ………….. (ii)
- Subtracting (ii) from (i)
![]()
(d) In an experiment to determine the specific latent heat of fusion of ice, heating coil is placed in a filter funnel and surrounded by lumps of ice. The following sets of reading were obtained.
| V(V) | 4.0 | 6.0 |
| I(A) | 2.0 | 3.0 |
| Mass of water m (g) collected in 500s | 14.9 | 29.8 |
Calculate
(i) Specific latent heat of fusion of ice (04marks)

(ii) Energy gained in the course of obtaining the first set of readings (03marks)

(e) Why re two sets of reading necessary n (d) above. (01mark)
To account for heat gained from surrounding
- (a) (i) State Dalton’s law of partial pressures. (01marks)
Dalton’s law of partial pressures states that the total pressure of a mixture of gases that do not react chemically is equal to the sum of partial pressures

(b) (i) What is meant by isothermal process and adiabatic process. (02marks)
Isothermal process is the expansion or compression of a gas at constant temperature.
Adiabatic process is the expansion or compression of a gas where there is no heat loss or gain into the gas.
(ii) Explain why adiabatic expansion of a gas causes cooling (03marks)
During an adiabatic expansion of a gas, no heat is supplied to the gas. Molecules strike the receding piston and bounce off with reduced velocities and hence lower kinetic energy. Since kinetic energy is proportional to temperature, the gas cools during the expansion
(c) A gas at a temperature of 170C and pressure 1.0 x 105Pa compressed isothermally to half its original volume. It is then allowed to expand adiabatically to its original volume
(i) Sketch a P-V curve the above process (02marks)
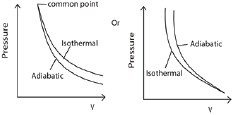
(ii) If the specific heat capacity at constant pressure is 2100Jmol-1K-1 and at constant volume is 1500Jmol-1K-1, find the final temperature of the gas (04marks)

(d) (i) What is meant by saturated vapour? (01mark)
A saturated vapour is a vapour in dynamic equilibrium with its own liquid.
(ii) Explain briefly the effect of altitude on the boiling point of a liquid (02marks)
A liquid boils when its saturated vapour pressure is equal to the external vapour pressure.
Atmospheric pressure decreases with increasing altitude, hence the boiling point of a liquid reduces as the altitude increases.
- (a)(i) Define a black body. (01mark)
A black body is a body which absorbs all the radiations incident on it and does not reflect or transmit any.
(ii) Sketch and explain graphs of intensity versus wavelength for three different temperatures of a black body. (03marks)
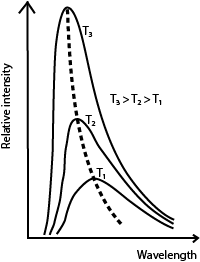
As temperature increases, the intensity increases. The intensity of shorter wavelengths increase more rapidly. The wavelength of the most intense radiation decreases as temperature increases.
(b)Describe with the aid of a diagram how an optical radiation pyrometer is used to measure temperature. (06marks)

- the filament is focused on the eye piece and the objective lens focuses the object so that the image of the object lies in the same plane as the filament
- Light from the hot object and the filament is passed through the red filter and viewed by the eyepiece.
- Current is adjusted by the rheostat R until the filament and the object are equally bright.
- The temperature of the hot body is then read from the calibrated ammeter, A.
(c) (i) State Prevost’s theory of heat exchanges (01marks)
When a body is in thermal equilibrium with its surrounding, its rate of emission of radiation to surrounding is equal to the rate of absorption of the radiation from the surrounding.
(ii) Metal sphere of radius 1.5cm is suspended within an evacuated enclosure whose walls are at 320K. The emissivity of the metal is 0.40. Find the power input required to maintain the sphere at a temperature of 320K, if heat conduction long the support is negligible. (04mrks)
(d) A metal boiler is 1.5cm thick. Find the difference in temperature between the inner and outer surfaces if 40kg of water evaporate from the boiler per meter squared per hour. [Latent heat of vaporization of water = 2268kJkg-1, Thermal conductivity of the metal of the boiler = 63Wm-1K-1] (05marks)
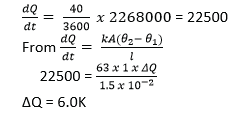
- (a) (i) State four desirable properties a material must have to be used as a thermometric substance. (02marks)
- The property must vary linearly with temperature
- The property must vary continuously with temperature
- The property must be easily measurable
- The property must be safe to handle
(ii) State why scales of temperature based on different thermometric properties may not agree. (01mark)
It is because different thermometric properties vary differently with temperature but only agree at the fixed points.
(b) With the id of diagram explain how a bolometer is used to detect thermal radiation. (06marks)

The bolometer strip is connected to Wheatstone bridge circuit above. The rheostat is adjusted until the galvanometer shows no deflection. When the radiations fall on the strip, they are absorbed and its temperature rises leading to an increase in resistance. The galvanometer deflects showing the presence of radiations.
(c) Describe, with the aid of a diagram an experiment to determine specific heat of vaporization of steam using the method of mixtures. (07marks)
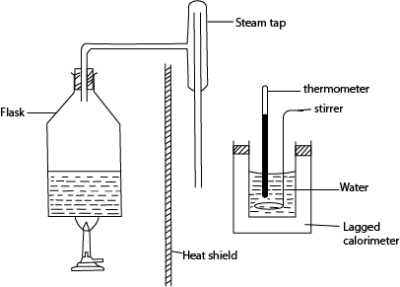
- The initial temperature θ0 and mass, m of water in the calorimeter are measured
- Steam from boiling water is passed into water in a calorimeter and after a reasonable temperature rise, flow of steam is stopped and final temperature, θf is recorded.
- Mass m2 of water in the calorimeter is then taken
- The mass of steam condensed, ms = (m2– m)
Given that the heat capacity of the calorimeter= C
Heat gained by steam = heat gained by water and calorimeter
mscv + msc(100- θf) = (m2 – m)c(θf – θ0) + C(θf – θ0)
cv = specific latent heat of vaporization
c= specific heat capacity of water
(d) A 600W electricity heater is used to raise the temperature of a certain mass of water in a thermos flask from room temperature to 800C. The same temperature rise is obtained when seam from a boiler is passed into an equal mass of water at room temperature in the same time. If 16g of water were being evaporated every minute in the boiler, find the specific latent heat of vaporization of steam, assuming no heat losses. (04marks)
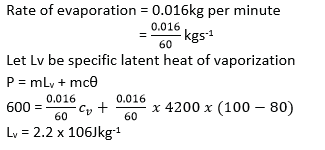
- (a) Define the following
(i) Absolute zero (01marks)
It is the temperature attained when molecules slow down and acquire the least possible energy
(ii) Cooling correction (01marks)
It is the temperature added to experimentally observed maximum temperature to cater for heat lost to the surroundings.
(b) (i) State Dalton’s law of partial pressures (01mark)
Dalton’s law of partial pressures states that the total pressure of a mixture of gases that do not react chemically is equal to the sum of partial pressures

(c) Explain clearly the steps taken to determine the cooling correction when measuring the specific heat capacity of a poor conductor by the method of mixtures. (07marks)
- Pour a liquid in a calorimeter and place it on a table
- Place a thermometer into the liquid and after sometime, record the temperature of the surroundings, θ0.
- Gently place a hot solid into the liquid and stir.
- Record the temperature of the mixture at suitable interval until the temperature of the mixture has fallen by about 10C below the observed maximum temperature, θ1.
- Plot a graph of temperature against time
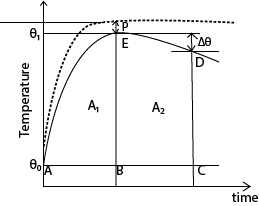
- The broken line shows how we would expect the temperature to rise if no heat were lost and the difference, P, between the plateau of this imaginary curve, and the crest of the experimental curve, E. is known as the ‘cooling correction’
- Draw a line AC through θ0 parallel to the time axis.
- Draw a line BE through θ1 parallel to the temperature axis.
- Draw a line CD beyond BE parallel to the temperature axis and note Δθ
- Estimate the area A1 and A2 under the graph by counting the square on the graph paper
- Cooling correction, P s given by the graph
![]()
- (a) Define thermal conductivity of material and state its units. (02marks)
Thermal conductivity is the rate of heat flow per unit area of cross section area per temperature gradient. Units are Wm-1K-1
(b) Describe an experiment to determine the thermal conductivity of copper. (06marks)

- Two holes are drilled into the copper specimen of mass m.
- A thermometer is inserted in one of the holes and an electric heater into the other hole. The holes are then filled with a good conducting fluid, e.g. oil to ensure thermal contact.
- The apparatus is insulated and initial temperature θ0 is recorded.
- The heater is switched on at the same time a stop clock is started.
- The steady values of ammeter reading, I and voltmeter reading, V are recorded.
- After considerable temperature rise, the heater is switched off and stop clock stopped.
- The highest temperature θ1 recorded and time t taken noted.
- The specific heat capacity, c, of the conducting solid is calculated from

(c) A double glazed window has two glasses each of thickness 4.0mm separated by a layer of air of thickness 1.5mm. If the two inner air-glass surfaces have steady temperature of 200C and 40C respectively. Find the
(i) temperatures of the outer air-glass surfaces (03marks)
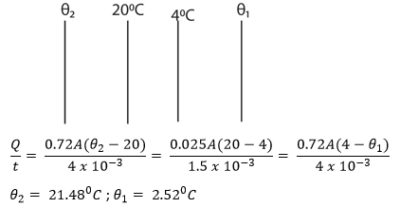
(ii) the amount of heat that flows across an area of the window of 2m2 in 2hours.
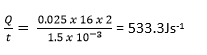
Heat flow in two hours = 533.3 x 2 3600 = 3.84 x 106J
[Conductivity of glass = 0.72Wm-1k-1 and that of air = 0.025Wm-1K-1]
(d)(i) What is a black body? (01mark)
A black body s one that absorbs all incident radiation falling on it and transmits or reflects none.
(ii) Explain how a welder can protect the eyes from damage. (03marks)
A welder puts on dark shades that absorb ultraviolet light which damages the eyes.
- Calculate the wavelength of the radiation emitted by a black body at 6000K
[Wen’s displacement constant = 2.9 x 10-3mK] (02marks)
λT = 2.9 x 10-3
6000λ = 2.9 x 10-3
λ = 4.8 x 10-7m
- (a) (i) State two differences between saturated and unsaturated vapours. (02marks)
- A saturated vapour pressure is one which is in dynamic equilibrium with its own liquid and an unsaturated vapour is one that is not in dynamic equilibrium with its own liquid.
- A saturate vapour pressure does not obey gas laws whereas unsaturated vapour approximately obey gas laws.
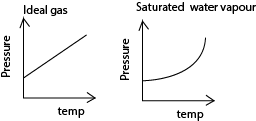
(ii) Sketch graphs of pressure against temperature for an ideal gas and for saturated water vapour originally at 00C (03marks)
(b) The specific heat capacity of oxygen at constant volume is 719Jkg-1K-1 and its density at standard temperature and pressure is 1.429kgm-3. Calculate the specific heat capacity of oxygen at constant pressure (04marks)

(c) (i) With the aid of a labelled diagram, describe an experiment to determine standard saturated vapour pressure of water. (05marks)

-
- The pressure of the air in R is shown by the mercury manometer; if its height is h, the pressure in mm mercury is P = H-h, where H is the barometer height.
- The tap is opened and the pressure above water varied using the pump to a suitable value.
- The tap is closed and water in the flask in heated until it boil.
- The temperature θ and difference in mercury levels, h, are noted and recorded.
- The saturated vapour pressure, P = (H± h) is calculated
- The procedure is repeated other values of θ and h
- A graph of P versus θ is plotted and it shows that saturated vapour pressure, P, increases with temperature, θ.
(ii) State how the experiment set up in (c) (i) may be modified to determine a saturated vapour pressure of above atmospheric pressure (01marks)
By replacing the vacuum pump with a bicycle pump
(d)(i) Define ideal gas (01mark)
An Ideal gas s one that obeys Boyle’s law under all conditions
(ii) State and explain the conditions under which real gases behave as ideal gases. (04marks)
- At higher temperature, the intermolecular spacing increases and intermolecular forces become negligible
- At very low pressure, the gas occupies negligible volume of the container.
- (a) (i) What is a black body?(01marks)
A black body is one which absorbs all the radiation that falls upon it, and reflects or transmits none.
(ii) Explain with the aid of a diagram how black body can be approximated. (03marks)
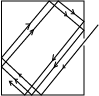
When radiation enters a black container through a hole, it undergoes multiple reflections. At each reflection, part of the radiation is absorbed. After several reflections, all the radiation is retained inside the container. Hence it approximates to a black body.
(iii) With the aid of sketch graphs explain the silent features of the spectral distribution of black body radiation (04 marks)

As temperature increases, the intensity increases. The intensity of shorter wavelengths increase more rapidly. At each temperature there is a wavelength for maximum intensity. The wavelength of the most intense radiation decreases as temperature increases.
(b) Give four properties of ultraviolet radiation. (02marks)
- produce ionization and florescence
- affect photographic plates
- produces photoelectric effect
- promotes chemical reaction
- can be reflected and refracted.
(c) Describe an experiment to compare the energy radiated by two surfaces at different temperatures (04marks)
- A metal cube whose sides have a variety of finishes; dull black, white, highly polished is filled with water and this water is kept boiling by a constant heat supply.
- A thermopile is made to face the various finishes of the cube at equal distances and each time the deflection on the galvanometer is noted.
- The deflection of the galvanometer is greatest when the thermopile is facing the dull-black surface and least when facing the highly polishes surface.
- This implies that the dull-black surface is a better radiator.
(d) (i) State Stefan’s law. (01mark)
Stefan’s law states that the total power radiated by a black body per unit surface area is proportional to the fourth power of its absolute temperature. i.e.
![]()
(ii) The earth receives energy from the earth from the sun at the rate of 1.4 x 103Wm-2. If the ratio of the earth’s orbit to the sun’s radius is 216, calculate the surface temperature of the sum. (05marks)

- (a) Define specific latent heat of vaporization. (01mark)
Specific latent heat of vaporization is the amount of heat required to change 1kg mass of a liquid into vapour at constant temperature.
(b) With the aid of labelled diagram, describe an experiment to measure the specific latent heat of vaporization of a liquid using an electrical method. (07marks)

- Put the liquid whose specific latent heat of vaporization is required in a vacuum jacketed vessel as shown above.
- The liquid is heated to boiling point.
- The current, I, and voltage, V are recorded.
- The mass of liquid, m, condensed in time, t, is determined.
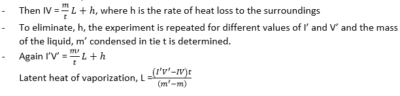
(c) Explain the effect of pressure on the boiling point of a liquid. (02marks)
- Since a liquid boils when its saturated vapour pressure is equal to external pressure.
- Increasing the external pressure increases the boiling point of a liquid because the liquid has to be heated to a higher temperature to make its saturated vapour pressure equal to external pressure.
(d) A liquid of specific heat capacity 2.8 x 103Jkg-1K-1 and specific latent heat of vaporization 9.00 x 105Jkg is contained in a flask of heat capacity 800JK-1 at a temperature of 320C. An electric heater rated 1kW is immersed in 2.5kg of the liquid and switched on for 12 minutes, calculate the amount of liquid that boiled off, given that the boiling point of the liquid is 800C. (06marks)
Heat supplied by the heater = mcθ + Cθ + m1L
1000 x 12 x 60 = 2.5 x 2.8 x 103(80-32) + 800 x (80- 32) + 9.00 x 105m1
Mass of the liquid evaporates, m1 = 0.384kg
(e) (i) Two thermometers are used to measure the temperature of a body. Explain why the temperatures may be different. (02marks)
Because thermometric properties vary differently with temperature and only agree at fixed points.
(ii) A platinum resistance thermometer has a resistance of 5.42Ω at the triple point of water. Calculate the resistance at a temperature of 50.00C. (02marks)

- (a) Define
(i) Specific heat capacity (01mark)
Specific heat capacity is the amount of heat required to rise the temperature of 1kg mass of a substance by 1K.
(ii) Specific latent heat of vaporization of a liquid. (01 mark)
Specific latent heat of vaporization is amount of heat required to convert 1kg of a liquid substance at its boiling point into vapor at constant temperature.
(b) With the aid of a labelled diagram, describe the electrical method of determining the specific heat capacity of a solid (07marks)

- Two holes are drilled into the solid specimen of mass m.
- A thermometer is inserted in one of the holes and an electric heater into the other hole. The holes are then filled with a good conducting fluid, e.g. oil to ensure thermal contact.
- The apparatus is insulated and initial temperature θ0 is recorded.
- The heater is switched on at the same time a stop clock is started.
- The steady values of ammeter reading, I and voltmeter reading, V are recorded.
- After considerable temperature rise, the heater is switched off and stop clock stopped.
- The highest temperature θ1 recorded and time t taken noted.
- The specific heat capacity, c, of the conducting solid is calculated from

(c) An electrical heater rated 48W, 12V is placed in a well-insulated metal of mass 1.0kg at a temperatures of 180C. When power is switched on for 5minutes, the temperature of the metal rises to 340C. Find the specific heat capacity of the metal (04marks)
Heat supplied by the heater, IVt = mcθ
48 x 5 x 60 = 1 x c x (34-18)
Specific heat capacity, c = 900Jkg-1K-1
(d) (i) State Newton’s law of cooling (01marks)
The rate of loss of heat is proportional to the excess temperature over the surroundings under conditions of forced convection.

Since for a given body, m and c are constant.
(e) Explain why evaporation causes cooling. (03marks)
During evaporation the most energetic molecules at the liquid surface escape leaving molecules with low kinetic energy. Since mean kinetic energy of molecules is directly proportional to absolute temperature, the liquid cools.
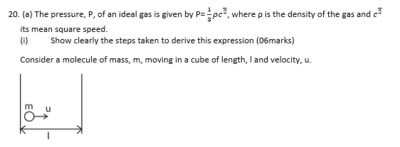

(ii) State the assumptions made in deriving this expression (02marks)
- Intermolecular forces of attraction are negligible
- The volume of the gas molecules are negligible compared to that of the container
- Molecules make perfectly elastic collision
- The duration of collision is negligible compared to the time between collisions
(b) Sketch the pressure versus volume curve for a real gas for temperatures above and below the critical temperature. (03marks)

- Above the critical temperature, a real gas behaves ideally.
- Below the critical temperature the turns into a liquid on compression as shown.
- A liquid is not compressible that is why pressure increases rapidly with a small decrease in volume.

b – accounts for the finite volume of molecules themselves.
(d) A balloon of volume 5.5 x 10-2m3 is filled with helium to a pressure of 1.10 x 105Nm-2 at a temperature of 200C. Calculate the
(i) the number of helium atoms in the balloon (03marks)
From PV =nRT
![]()
Number of atoms = 2.48 x 6.02 x 1023 = 1.49 x 1024.
(ii) net force acting on the square meter of material of the balloon if the atmospheric temperature is 1.01 x 105Nm-2 (04marks)
F = PA
Net force = internal force in the bulb – external force on the bulb
= (1.10 x 105 – 1.01 x 105) x 1.0 = 9.0 x 103N
- (a) (i) Define thermal conductivity of a material (01mark)
Thermal conductivity is the rate of heat flow through a material per unit cross sectional area per unit temperature gradient.
(ii) Describe an experiment to determine the thermal conductivity of copper. (06marks)

- Two holes are drilled into the solid specimen of mass m.
- A thermometer is inserted in one of the holes and an electric heater into the other hole. The holes are then filled with a good conducting fluid, e.g. oil to ensure thermal contact.
- The apparatus is insulated and initial temperature θ0 is recorded.
- The heater is switched on at the same time a stop clock is started.
- The steady values of ammeter reading, I and voltmeter reading, V are recorded.
- After considerable temperature rise, the heater is switched off and stop clock stopped.
- The highest temperature θ1 recorded and time t taken noted.
- The specific heat capacity, c, of the conducting solid is calculated from

(b) (i) What is a black body? (01 marks)
A black body is one which absorbs all the radiation of every wavelength falling on it, reflects and transmits none.
(ii) Describe how infrared radiation can be detected using a bolometer. (03marks)

The bolometer strip is connected to Wheatstone bridge circuit above. The rheostat is adjusted until the galvanometer shows no deflection. When the radiations fall on the strip, they are absorbed and its temperature rises leading to an increase in resistance. The galvanometer deflects showing the presence of radiations.
(ii) Give one characteristic property of infrared radiation. (01mark)
Causes sensation of warmth (increases body temperature.
(c) (i) A spherical black body of radius 2.0cm at -730C is suspended in an evacuated enclosure whose walls are maintained at 270C. If the rate of exchange of thermal energy is equal to 1.85Js-1, find the value of Stefan’s constant, (05marks)

(ii) Calculate the wavelength at which the radiation emitted by the enclosure ha maximum intensity (03mark)
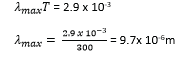
Please obtain free notes, exams and marking guides of Physics, chemistry, biology, history, economics, geography … from digitalteachers.co.ug website.
Compiled by Dr. Bbosa Science
Sponsored The Science Foundation College +256 753 802709

Very nice notes
Very nice notes and it will be better if downloadable
download from the main menu
Great work done
Choose our Airport Shuttle Houston to Galveston for effortless transportation to the Galveston Cruise Terminal and beyond. Enjoy reliable service from Houston’s airports, including connections to Kemah Boardwalk, Downtown Houston, League City, and Clear Lake. Reserve your shuttle today!
Choose our Luxury Parry Sound Taxi Service to Toronto for an elegant and smooth ride. Whether you’re booking a Taxi to Parry Sound Airport or a Transfer from Parry Sound Airport, we provide high-end transport with professional drivers. Our Limo to Parry Sound Airport is also available for ultimate comfort.
Shuttle transportation is an economical option for those who don’t mind sharing a ride with fellow travelers and making multiple stops. If you have any questions, please call Airport Transfer Bahamas
Experience the convenience of our Owen Sound Airport Transfer Service. We offer reliable shuttle services from Owen Sound to Toronto Pearson, affordable taxis to Kitchener Airport, and private limo transfers to Billy Bishop. Our executive limo service ensures a luxurious, comfortable experience for all your airport travel needs.
Celebrate in style with our luxury West Palm Beach party buses. Affordable and perfect for weddings, proms, and events, our rentals offer premium comfort, modern amenities, and great service. Experience elegance at unbeatable prices. Make your event unforgettable—book your West Palm Beach party bus rental today!
Party Bus Miami creates unforgettable memories for your special moments. From Miami Party Bus Rentals to Miami Prom Luxury Bus Service, enjoy stylish and affordable transportation. Perfect for weddings, birthdays, and bachelor/bachelorette parties.
Elevate your events with Party Bus Miami. Enjoy Miami Party Bus Rentals tailored for birthdays, weddings, and bachelor/bachelorette parties. Choose options like Wedding Party Bus Miami or Miami Prom Luxury Bus Service for a memorable ride in comfort and style.
Explore wheelchair-accessible car services and group transportation alternatives in Washington DC. With a plethora of options, including shuttles and general transportation, the capital ensures seamless travel experiences. Consider KVLIMO for top-tier transportation solutions that prioritize comfort and reliability.
For luxury and safety in transportation, Airport Transfers Bahamas offers a distinguished fleet. Each vehicle is designed for comfort and adheres to strict safety standards for your peace of mind.
Bahamas Premium Transfers is proud to serve private transportation from Nassau Airport to Paradise Island with professional cheuffeur. As a leader in transportation and special event chauffeur services,
Bahamas Premium Transfers is proud to serve private transportation from Nassau Airport to Paradise Island with professional cheuffeur. As a leader in transportation and special event chauffeur services,
Our Miami prom party bus rental offers the best prom limo bus Miami experience. Choose from Miami prom night bus rental options and enjoy affordable prom party bus Miami packages. Experience premium prom transportation Miami with our Miami luxury prom party bus for memorable Miami prom group transportation.
Airport Transfer nassau offers reliable, affordable transportation from Nassau Airport to the beautiful Baha Mar.
Our Niagara Falls airport shuttle service ensures comfortable travel to and from Niagara Falls Airport, Buffalo Airport, and Toronto Pearson. We offer reliable shuttle rides and convenient transfers to local hotels, providing a smooth travel experience every time.
Burlington To Pearson Airport Taxi – Your ideal choice for efficient travel. Airport Limo Burlington ensures a comfortable ride to Toronto Pearson Airport. Trust Burlington Cab Company for reliable service.
Effortlessly traverse between Buffalo and Mississauga with our dedicated Airport Limo and Taxi Services. From Buffalo Airport to Mississauga, enjoy punctual transportation ensuring a smooth transition. Reserve your ride today for stress-free travel.
Rent a professional limousine service in Dubai with safety equipments
Choose Van Services Dubai for comfortable and Affordable Van Services Dubai. Whether you need a Van with Driver Dubai for airport transfers or a Chauffeur Van Service Dubai for events, we’ve got you covered.
Enjoy a stress-free Dubai Airport to Hotel Transfer to Atlantis The Palm. Our services, including Taxi from Dubai Airport to JBR Hotels and Dubai Airport to Atlantis Hotel Shuttle, provide reliable and comfortable options for all travelers.
Little Stars Travel offers luxury car services in Dubai, providing a premium transportation experience for a stylish and comfortable journey.
Experience luxury with our professional Chauffeur Car Service in Chicago. Whether for corporate events, weddings, or leisure outings, our chauffeurs provide top-notch service. With our executive sedans and reliable chauffeurs, arrive in style and comfort.
Experience luxury travel with our Limo Bus Winnipeg services. From weddings to corporate events, our Affordable Limo Bus Winnipeg guarantees comfort and style. Whether it’s a Prom Limo Winnipeg or a Winnipeg to Kenora Limo Service, enjoy exceptional convenience for every occasion. Book your Party Bus Limo Winnipeg today!
Travel in style with our Luxury Car and SUV transportation services, featuring Luxury SUV transportation across Los Angeles County. We offer reliable rides from Rancho Cucamonga to LAX, Orange County, Riverside County, and luxury trips to Disneyland and Los Angeles.
From private car services to luxury options, Houston to Galveston shuttles cater to different needs. Travelers can choose between black car, corporate, VIP express, or cruise shuttle services, ensuring smooth airport transfers or transportation for special occasions and groups.