
Refraction through the convex and concave lenses (A-level physics)

Refraction through lenses
A lens is a piece of glass bounced by one or two spherical surfaces.
Lenses are of two types namely;
(i) Convex (Converging) lens: It is a lens which is thicker in the middle than at the edges.

(b) Concave (Diverging) lens: It is a lens which is thinner in the middle than at the edges.

Definitions
1. Centres of curvature of a lens: These are centres of the spheres of which the lens surfaces form parts.
Points C1 and C2 are the centres of curvature of the lens surfaces.
2. Radii of curvature of a lens: These are distances from the centres to the surfaces of the spheres of which the lens surfaces form parts.
3. Principal axis of a lens: This is the line joining the centres of curvature of the two surfaces of the lens.
4. Optical centre of the lens: This is the mid-point of the lens surface through which rays incident on the lens pass un-deviated.
5. Paraxial rays: These are rays close to the principal axis and make small angles with the lens axis.
6. (i) Principal focus “F” of a convex lens: it is a point on the principal axis where paraxial rays incident on the lens and parallel to the principal axis converge after refraction by the lens.
(ii) Principal focus “F” of a concave lens: it is a point on the principal axis where paraxial rays incident on the lens and parallel to the principal axis appear to diverge from after refraction by the lens.
7.(i) Focal length “f” of a convex lens: it is the distance from the optical centre of the lens to the point where paraxial rays incident and parallel to the principal axis converge after refraction by the lens.
(ii) Focal length “f” of a concave lens: it is the distance from the optical centre of the lens to the point where paraxial rays incident and parallel to the principal axis appear to diverge from after refraction by the lens.
Geometrical rules for the construction of ray diagrams
The following is a set of rules for easy location of the images formed by lenses:
(i) A ray parallel to the principal axis after refraction passes through the principal focus or appears to diverge from it.
(ii) A ray through the principal focus is refracted parallel to the principal axis.
(iii) A ray through the optical centre continues straight or un-deviated.
NOTE:
(i) The normal to the lens surfaces must pass through its centres of curvature.
(ii) The image position can be located by the intersection of two refracted rays initially coming from the object.
Images formed by a convex lens
The nature of the image formed by a convex lens is either real or virtual depending on the object distance from the lens as shown below;
(a) Object is between F and P
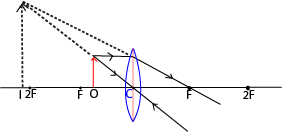
The image is magnified, virtual, erect
(b) Object at F

The image is real, inverted, magnified and at infinity
(c) Object between F and 2F

The image is real, beyond C, inverted and magnified
(d) Object at 2F
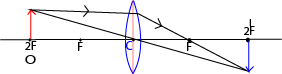
The image is real, inverted, same size as the objec
(e) Object at infinity

The image is real, inverted and diminished
Note;
Generally the image of an object in a convex lens is virtual only when the object is nearer to the lens than its focus.
Uses of convex lenses
- They are used in spectacles for long-sighted people
- They are used in cameras.
- They are used in projectors.
- They are used in microscopes.
- They are used in astronomical telescopes.
Images formed by a concave lens
The image of an object in a convex lens is erect, virtual, and diminished in size no matter where the object is situated as shown below

The image is virtual, erred and diminished
Uses of concave lenses
- They are used in spectacles for short-sighted people
- They are used in Galilean telescopes.
Lenses compared with prisms
A thin lens may be regarded as being made up of several portions of small-angle prisms placed together as shown:

All paraxial rays incident on the lens at a single point suffer a similar small deviation D = (n– 1) A produced by a prism of small-angle A regarded to have replaced the lens.
Lenses and sign convention
In order to obtain a formula which holds for both concave and convex lenses, a
Sign rule or convention must be obeyed and the following shall be adopted.
(i) Distances of real objects and images are positive.
(ii) Distances of virtual objects and images are negative.
NOTE:
A convex lens has a positive focal length while a concave lens has a negative focal length.
The thin lens formula
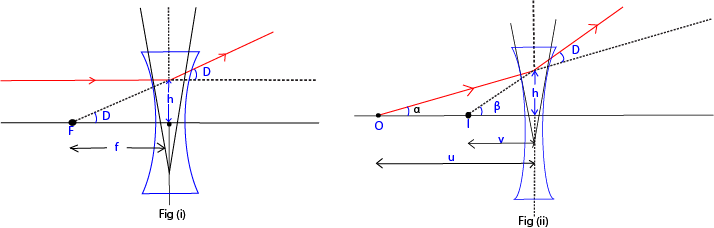
Consider in each case a paraxial ray incident on the same lens at a small height h above the principal axis as shown:

From Fig (i), the ray is converged to the focal point F to suffer a small deviation D

This is the general lens equation.
If the sign conversion is used for u, v and f the equation holds for both converging and diverging lenses.
NOTE:
The same result above can be derived with the aid of a concave lens having light ray paths shown below:
Example 1
Derive the relationship between focal length f , object distance u and image distance v for a thin lens
Example 2
An object is placed 20cm from
(a) A converging lens, f = 15cm
(b) Diverging lens of focal length 15cm. Calculate the position and nature of image formed in each case

Power of a lens
This is the reciprocal of the focal length of the lens in meters. It is measured in dioptres.
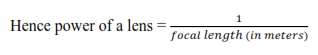

NOTE:
The power of a converging lens is positive while that of a diverging lens is negative.
Example 3
Calculate the power of a converging lens of focal length 25cm.
Solution
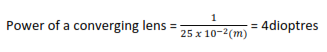

Example 4
Calculate the power of a diverging lens of focal length 20cm.
Solution
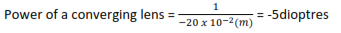

Formula for magnification


Proof
Consider a lens l, which forms an image I of height h’, at distance v from the lens of object an object, O of height, h, placed a distance u, from the lens.
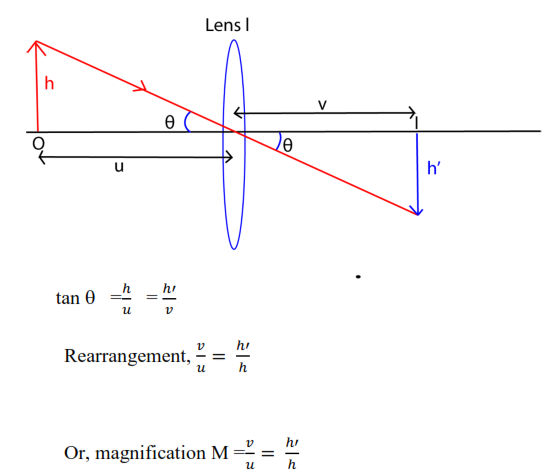
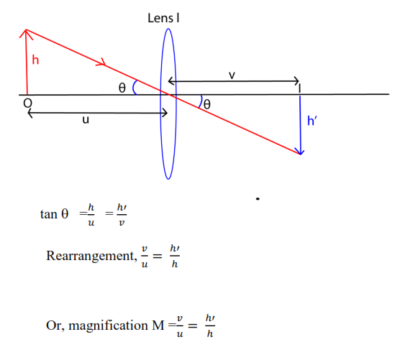
Relationship connecting m, v and f
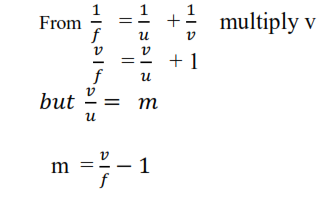
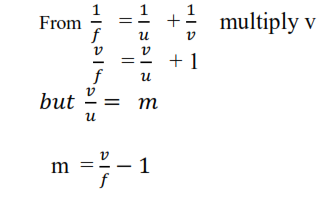
Minimum separation of an object and its real image formed by a convex lens
Consider a real image I of an object O formed by a convex lens of focal length f as shown:

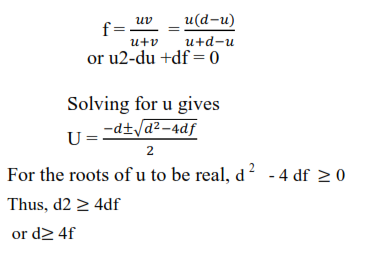
Thus, the minimum distance between the screen and object must be greater than 4f which implies that 4f is the minimum distance between the real image and the object.

Relationship between focal length, radii of curvature and refractive index of a lens
Consider a ray parallel to the principal axis, incident at height, h.


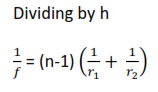
Conjugate points
These are two points each on the opposite side of a convex lens such that an object and its image at these points are interchangeable.
NOTE:
The property of conjugate points is such that when an object is placed at one of the points, the image is formed at the other point by the lens.
Newton’s formula (Newton’s relation)
Consider an object, O, such that its image, I, is formed


Combined focal length of two thin lenses
Consider two thin lenses L1 and L2 of focal length f1 and f2.
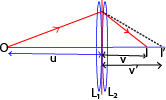
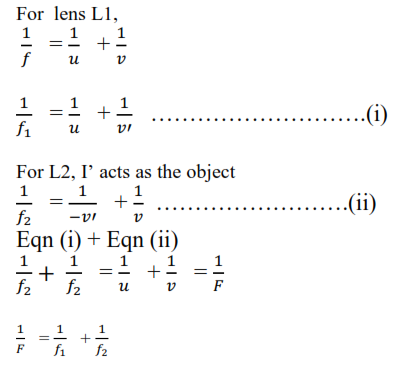
Where F is the focal length of combined lens,
Determination of focal length of convex lens
(a) Determining the focal length of a convex lens using displacement of a convex lens when O and I are fixed

Lens A forms an image of O at I
By the principle of reversibility of light, an object at I forms an image at O. when the object and the screen are fixed, another clear image can be formed by the lens when moved from A to B.

(b) Measuring the focal length of convex lens using a lane mirror method (Non parallax method)
- Place a plane mirror M on a table and lens L on top of it.
- Clamp a pin, O, horizontally with its tip lying horizontally along the principal axis of the lens
- Move the pin O up and down along the principal axis to locate the position where it coincides with the image.
- Measure the focal length, f, a distance from the pin to the lens .
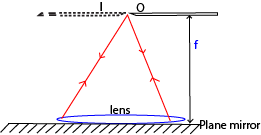
(c) Determining the focal length of a convex lens by focusing a distant object.
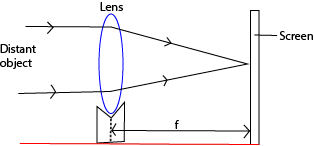
- Position the lens to sharply focus a distant object on the screen
- Measure the focal length f.
(d) Determining the focal length of a convex lens using the lens formula (experimental method)

(i) Using illuminated object at measured distance from the lens, move the lens to and fro the lens until a clearly focused wire gauze forms on the screen and measure distance, d.
(ii) Repeat the procedure for several values of u and each time measure the distance v.
(iii) Tabulate your results
| u(cm) | V (cm) | (u+v) (cm) | uv (cm2) | ||
(a)A plot of 1/u against 1/v gives a shape of the graph below

(b) A plot of uv against (u+v)

Example 5
A thin converging lens of 6cm focal length is placed in a container with a diverging lens of focal of focal length 10cm. find the focal length of the combined lenses.
Solution
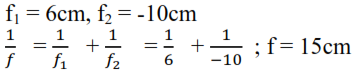
Example 6

(b) A thin lens with faces of small radii of curvature 20cm and 30cm is to be made from glass with refractive index 1.6. What is the focal length of the lens if it is
(i) biconvex
(ii) biconcave
Solution
(a) Refer to the notes above
(b) (i)

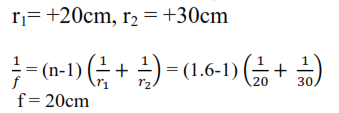
(ii)
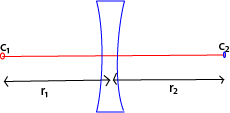

Example 8
Calculate the focal length of a converging meniscus with radii 25cm and 20cm with refractive index 1.5
Solution

Example 9

In the diagram above, the image of the object formed on the screen when a convex lens is placed either at A or B. if A and B are 15cm apart, find
(i) The focal length of the lens
(ii) The magnification of image formed at B.



Solution

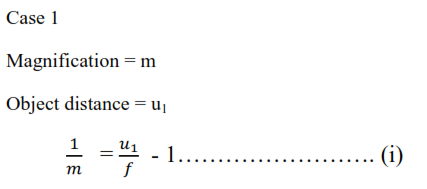
Case II

Example 12
A point screen is placed 125cm from a luminous object. A converging lens is placed between the object and the screen at a distance of 75cm from the screen such that a clear image is obtained on a screen. Find the height of the object given that the height of the image is 8cm.

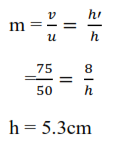
Determining the refractive index of a small quantity of a liquid using a convex lens and plane mirror.
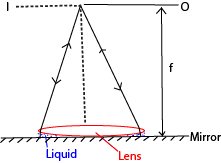
(i) pour a small liquid on the plane mirror and place the convex lens on top.
(ii) Move the object, O, along the principal axis until it coincides with its image, I.
(iii) Measure the distance, F, from O to the lens which is the combination of the focal length of the liquid and the lens.
(iv) Repeat the experiment (ii) with the convex lens and the plane mirror without the liquid and determine focal length, f, of the glass lens
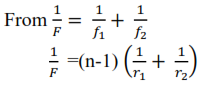
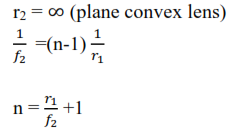
Example 12
A biconvex lens of radius of curvature 24cm is placed on a liquid film on a plane mirror. A pin clamped horizontally above the lens coincides with its image at a distance of 40cm above the lens. If the refractive index of the liquid is 1.4. What is the refractive index of the material of the lens?
Solution


Example 13
An equi-convex lens of refractive index 1.54 is placed on a horizontal plane mirror. A pin is moved along the horizontal axis of the lens and is found to coincide with its image at 25cm above the lens. The lens is then floated on the surface of mercury in a dish and coincides between the pin and its image is again obtained at height, h, above the lens. Find the value of n given that the refractive index of mercury is 1.42.
Solution

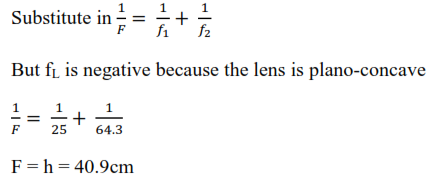
Exercise
- Two eqiconvex lenses of focal length 20cm and mad eof glass of refractive index 1.6 are placed in contact and the space between them is filled with a liquid of refractive index 1.4. Find the focal length of the lens combination. [Answer f =15cm)
- A thin equi-convex lens of glass of refractive index =1.5whose surfaces have radii of curvature 24cm is placed on a horizontal plane mirror when the space between the mirror and the lens is filled with a liquid, a pin placed 40 cm vertically above the lens coincides with its image. Calculate the refractive index of the liquid. [Answer: nL = 1.4)
- The curved face of a plano convex lens of refractive index 1.5 is placed in contact with a plane mirror. A pin placed at distance 20cm coincides with its image. A film of a liquid is now introduced between the lens and the plane mirror. Then the coincidence of the pin and its image is found to be at a distance 100cm. calculate the refractive index of the liquid. [Answer: nL =1.4)
- A small quantity of a liquid of refractive index 1.4 is poured on a horizontal plane mirror and biconvex lens of focal length 30cm and refractive index 1.5 is then place on top of the liquid. The pin is moved along the axis of the lens until no parallax between it and its image. Find the distance between the pin and lens. [Answer: 50cm)
Determination of focal length of concave lens
(a) Determination of focal length of concave lens using convex lens
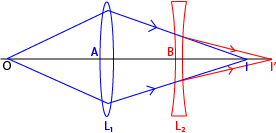
I’- is the virtual object of lens L2.
I – is a real image of lens L1
(i) An object, O, is placed at a distance greater than f of lens L1.
(ii) The image formed by L1 is I is the virtual object to lens L2. Measure the distance AI.
(iii) Lens L2 is then placed between L1 and I and a real image I’ is formed by L2. Measure the distance AB and BI and BI’
(iv) Image distance, v = BI’, and object distance, u = BI = AI – AB which is negative.
(v) The focal length L2 is calculated from

Example 14
A converging lens L1 of focal length 10cm is placed at a distance, y, in front of a diverging lens L2 of focal length 20cm. An illuminated object is placed at a distance of 20 cm in front of L1 and the final image by L2 formed at the principal focus of L2. Calculate the
(i) Distance y
(ii) Final magnification
Solution

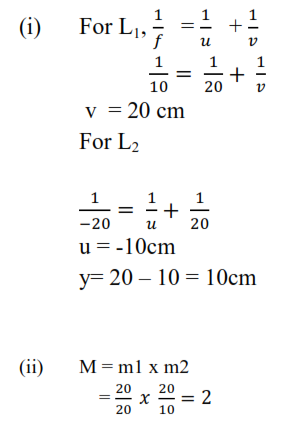
Exercise
An object is placed 6cm from a thin converging lens, A, of focal length 5cm. Another thin converging lens B of focal length 15cm is placed co-axillary with A and 20cm from it on the side away from the object. Fins the
(i) Position
(ii) Nature and
(iii) Magnification of the image.
[answer ((i) 6cm from B. m = 3. ]
(b) Determination of focal length of concave lens using concave mirror.

(i) An illuminated object is placed beyond the center of curvature of a concave mirror of known radius of curvature , r.
(ii) A diverging less L is placed between O and M and its position is adjusted until a clear image I is formed besides O.
(iiii) Distance LI and LM are measured and recorded.
(iv) For the lens, object distance, u = -CL = – (r-LM); image distance, v =LI or LO

Lens defects
(i) Spherical aberration where rays of light are not focus at a single point resulting in blurred image.
(ii) Chromatic aberration where white beam of light produces blurred colored images.

I carry on listening to the news update lecture about getting free online grant applications so I have been looking around for the best site to get one. Could you tell me please, where could i acquire some?
Nice blog here! Also your website loads up very fast! What web host are you using? Can I get your affiliate link to your host? I wish my website loaded up as fast as yours lol
Thanks for being so informative and clear. Electronics
Thanks for being a beacon of knowledge. Top adult movies
Streamline your medical college application with MBBS Direct Admission in Andhra Pradesh.
Get personalized guidance for MBBS Admission Through Management/Nri Quota in Manipur.
Test your skills and luck with the immersive Raja Luck Game.
Learn how Raja Luck is evolving over time.
Enjoy 24/7 client support and help at 82 Lottery for a problem-free experience.
Outstanding write-up on Nainital’s destinations! For night social plans, Escort Service In Nainital can organize wonderful company.
The payout system of 82 lottery is quite quick, making it a reputable option.
The quick processing of Youtube To MP3 Converter makes it stand apart from the rest.
Every time I visit https://www.youtube.com/@kpopbuzzindo/shorts, I find something new to love about K-pop!