Simple harmonic motion

It a special type of periodic motion in which the acceleration of the body along the path of the body is directed towards a fixed point in the line of motion and is proportional to the displacement of the body from a fixed point

Characteristic of a body describing simple harmonic motion

• Motion is periodic
• Acceleration of the body is towards a fixed point
• Acceleration of the body is directly proportional to the distance from the fixed point
• Mechanical energy is conserved

 

Equation of simple harmonic motion

Acceleration, a = – ω²x

Where ω is the angular velocity, x, is a displacement from fixed point

Or  a =  = – ω²x

The solution of above differential equation is

x = Acos ωt or x  = Asin ωt

where A is the maximum displacement of the body from the rest position the  called

Amplitude

x is the displacement of the body at any time t.

For x = Asin ωt, the curve is given below

 In general x = Asin(ωt + Ф) where Ф is the phase angle

Examples of simple harmonic motion

(i) Vertical spiral spring or Elastic thread

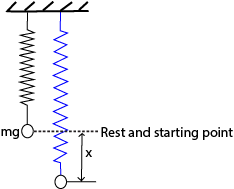
Consider a body of mass, m suspended from a spiral spring of force constant, k, as shown in the diagram above.

In that case the body will be in equilibrium

At equilibrium, T = mg

But T = ke (From Hooke’s law)

Where e is the extension in the spring at equilibrium and k is the force constant of the spring.

Hence  ke = mg ……………………………………….. (i)

When the mass is pulled through a distance x, then released, the resultant upward force on the mass is

F = T’ –mg

But T’ = k(e + x)

F = k (e + x) – mg

From (i) ke = mg

F = k(e + x) – ke

F = kx

From Newton’s 2^nd law, ma = F

ma  = -kx

(ii) Horizontal spring

When a spring  is stretched by a distance, x.

The resultant force = 0 –T

Since at equilibrium there is no force.

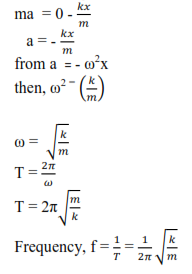
(iii) Simple pendulum

Suppose a body of mass, m, attached to a string is displaced through a small angle θ and then released. The resultant force on the body towards O is mgsinθ.

 

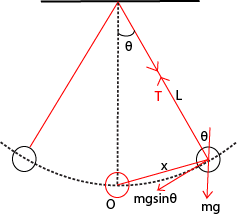
By Newton’s 2^nd law

ma = – mgsinθ

a = -gsinθ

(iv) U-shaped tubes

A liquid of density ρ contained in a U-tube of cross-section area A and column L, if the liquid is displaced slightly through a distance x from equilibrium position

 

The restoring force of the liquid = 2xAρg

(v) A floating cylinder

Consider a cylinder of mass, m, floating vertically in a liquid of density, ρ, to a depth, L

 

At equilibrium position, the body sinks to a height, h, below the liquid surface

Up thrust = weight of the body

But U = Ahρg

mg = Ahρg ……………………………………..(i)

A is the cross-section area of a cylinder

When a body is displaced through a distance, x, and released,

Up thrust = (h + x) Aρg

Resultant force = mg – (h + x) Aρg

But, m = Ahρ

ALρa  = Ahρg – Ahρg – Aρgx

Velocity of a body executing simple harmonic motion

The displacement of the body executing simple harmonic motion is given by

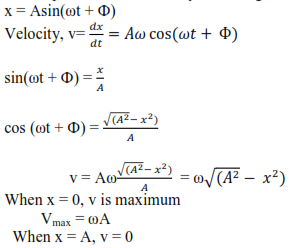
Kinetic energy and potential energy of vibrating object

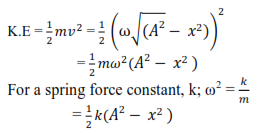
Potential energy, P.E

Work done against restoring force is potential energy

F = mω²r

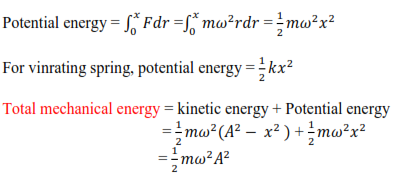
Example 1

A light spiral spring is loaded with a mass of 50g and it extends by 10cm. Calculate the  period of small vertical oscillations.

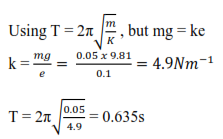
Example 2

A body of mass 0.1kghangs from a long spiral spring. When pulled down 10cm below its equilibrium point, A and released, it performs simple harmonic motion with a period 2s

(a) What is the velocity as it passes through A?

(b) What is its acceleration when it is 5cm above A.

Solution

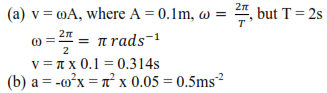
Types of oscillations

(i) Free oscillations

Free oscillations occur in absence of any dissipative force like air resistance, friction, and viscous drag. The Amplitude and total mechanical energy remain constant and the system oscillates indefinitely with a period T (the natural period of vibration of the system

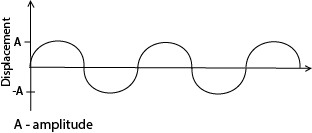
e.g. a simple pendulum will undergo free oscillation in a vacuum

(ii) Damped oscillations

These are oscillations where the system loses energy to the surroundings due to the dissipative forces. The amplitude reduces with time an be grouped into underdamped, critically damped and overdamped oscillation.

• Under-damped oscillation

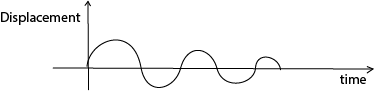
The system oscillates but gradually dies out due to the dissipative forces. The amplitude of oscillation decreases with time. Examples are a simple pendulum in air, horizontal spring moving over a surface of little roughness.

• Critically damped oscillation

The system does not oscillate when displaced, but returns to equilibrium position in the minimum possible time.

Example: a horizontal spring moving over a very rough surface, a metal cylinder attached to a vertical spring and mad to move in a very viscous liquid.

 

Example 4

(a) (i) What is meant by simple harmonic motion

(ii) state two practical examples of simple harmonic motion

(iii) using two graphical illustrations, distinguish between the underdamped oscillation

(b) (i) Describe an experiment to measure the acceleration due to gravity using a spiral spring.

(ii) State two limitation to accuracy of the value in (b)(i).

(c)  A horizontal spring of force constant 200Nm^-2 fixed at one end has a mass of 2kg attached to the free end and             resting on a smooth horizontal surface. The mass is pulled through a distance of 4.0cm and released. Calculate

(i) Angular speed

(ii) Maximum velocity attained by the vibrating body

(iii) Acceleration when the body is halfway towards the center of the initial position.

Solution

(a) (i) It a special type of periodic motion in which the acceleration of the body along the path of the body is directed             towards a fixed point in the line of motion and is proportional to the displacement of the body from a fixed                   point

(ii) – motor vehicle inspection spring

–  Atom vibrating in a crystal

(iii) underdamped

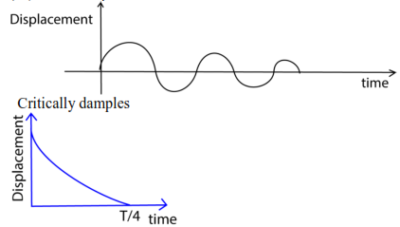
If a system is underdamped, the amplitude of oscillation decrease with time due to energy loss in doing work against the dissipative forces; whereas for critically damped oscillation the time taken for the displacement to be zero is minimum and it is equal to ¼ of the periodic time, T.

 

(b) (i) Known mass, mass hanger, meter rule, pointer, retort stand and stop clock.

The set up is shown below

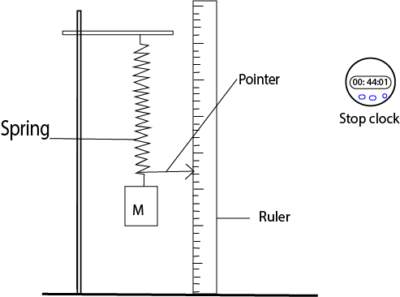
1. A mass M is loaded the spring and extension x is recorded.
2. The mass is given a slight displacement, time for twenty oscillations, t, is noted.
3. Period of the oscillation, T, and T² are calculated.
4. The procedures a. to d. for several masses are repeated.
5. A graph of T² against x is plotted as a slope of the graph, s, is calculated.

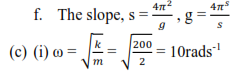
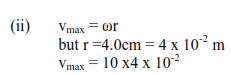
(iii) Since a = – ω²x

x = 2cm = 2 x 10^-2m

a = – 10² x 2 x 10^-2

             a = 2ms^-2

Example 5

(a)(i) What is meant by a simple harmonic motion?

(ii) Distinguish between damped and forced oscillation.

(b) A cylinder of length, l, cross-section area A and density, σ, floats in a liquid of density. The cylinder is pushed              down slightly and released.

(i) Show that it performs simple harmonic motion

(ii) Derive the expression for the period of oscillation

(c) A spring of force constant 40Nm^-2 is suspended vertically, A mass 0.1kg suspended from the spring is pulled               downward a distance of 5mm and released. Find the

(i) Period of oscillation

(ii) Maximum acceleration of the mass

(iii) Net force acting on the mass when it is 2mm below the center of oscillation.

Solution

(a)(i) It a special type of periodic motion in which the acceleration of the body along the path of the body is directed towards a fixed point in the line of motion and is proportional to the displacement of the body from a fixed point.

(ii) Damped oscillation are oscillation in which the amplitude of oscillation decreases due to the presence of dissipative forces like friction.

Forced oscillation is those where external force only is required to keep the system in perpetual oscillation.

(c)(i)     

At equilibrium position, the body sinks to a height, h, below the liquid surface

Upthrust = weight of the body

But U = Ahρg

mg = Ahρg ……………………………………..(i)

A is the cross-section area of a cylinder

When a body is displaced through a distance, x, and released,

Upthrust = (h + x) Aρg

Resultant force = mg – (h + x) Aρg

But, m = Ahσ

ALσa  = ALρg – Ahρg – Aρgx

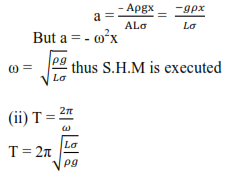
(c) (i) the acceleration of the spring-mass system is given by

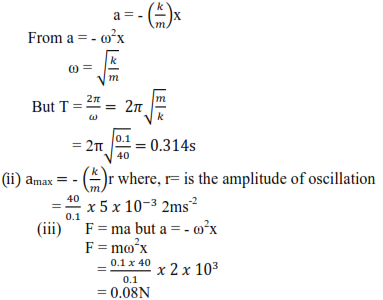
Example 6

(a) What is meant by simple harmonic motion?

(b) A cylindrical vessel of cross section, a, contains air of volume, V, at pressure P, trapped by frictionless air tight               position of mass, M, the position is pushed down and released.

(i) If the position oscillates with simple harmonic motion, show that the frequency is given by

(ii) Show that the expression in (b)(i) is dimensionally correct.

(c)  A particle executing simple harmonic motion vibrated in a straight line. Given that the speed of the particle is                4ms^-1 and 2ms^-1 when the particle is at 3cm and 6cm respectively from equilibrium, calculate

(i) Amplitude of oscillation

(ii) Frequency of the particle.

(ii) Give two examples of oscillating motion which approximate to simple harmonic motion and state the                             assumptions made in each case.

Solution

(a) It a special type of periodic motion in which the acceleration of the body along the path of the body is directed              towards a fixed point in the line of motion and is proportional to the displacement of the body from a fixed point.

(b)

At equilibrium, force  = PA

PA = Mg …………………………….. (i)

Suppose it is pushed through a small distance x and pressure changes to P’

Restoring force, F= P’A – Mg ……………………… (ii)

Using Eqn. (i) and Eqn. (ii)

Hence Ma = (P’A –PA) ……………………………  (iii)

From Boyles’ Law, P₁V₁ = P₂V₂

P’(V –Ax) =PV

Since LHS = RHS, the expression is dimensionally consistent.

(c)(i) from v² = ω²(r²-x²)

4² = ω² (r² – 0.03²)

16 = ω² (r² – 0.0009) …………………………….. (i)

Also    4 = ω² (r² – 0.06²)

= ω² (r² – 0.0036) ……………………………… (ii)

Eqn. (i)  Eqn. (ii)

(d) (i) The oscillation of a simple pendulum when the angle of displacement is very small and air resistance is negligible.

(ii) The mass oscillating at the end of spiral spring when the displacement from equilibrium solution is very small and dissipative force is negligible.

Example 7

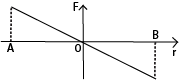
(a)(i) Define simple harmonic motion.

(ii) A particle of mass m executes simple harmonic between two points A and B about equilibrium position O. Sketch a graph of the restoring force acting on a particle as a function of distance, r, moved by the particle.

(b)

Two springs A and B of spring constant K_a and K_b respectively are connected to a mass as shown in the figure above. The surface of which the masses slide is frictionless.

(i) Show that the mass is displaced slightly. It oscillates with simple harmonic motion of frequency, f, given by

(ii) If the two springs are identical such that Ka = Kb = 5.0Nm^-1 and mass, m = 5.0g.

Calculate the period of the oscillation.

Solution

(a) (i) It a special type of periodic motion in which the acceleration of the body along the path of the body is directed towards a fixed point in the line of motion and is proportional to the displacement of the body from a fixed point.

(ii)

(b)(i) Suppose the body is displaced through a small distance x towards B

Resultant force, F = K_ax + K_bx

ma  = K_ax + K_bx

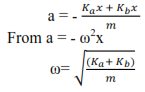
Example 8

(a) Define simple harmonic motion.

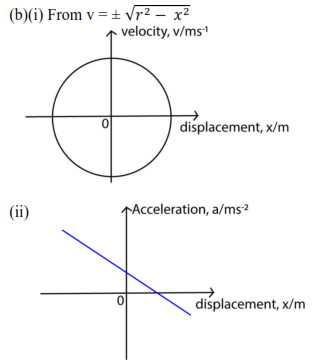
(b) Sketch a graph of

(i) Velocity against displacement

(ii) Acceleration against displacement for a body executing S. H.M.

(c) A glass U- tube containing a liquid is tilted slightly and then released

(i) Show that the liquid oscillated with S.H.M.

(ii) Explain why oscillations ultimately come to rest.

Solution

(c)

 

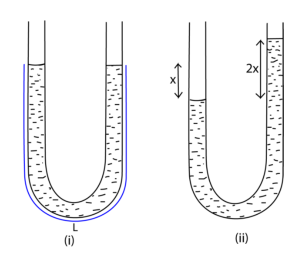
A liquid of density ρ contained in a U-tube of cross-section area A and column L, if the liquid is displaced slightly through a distance x from an equilibrium position

The restoring force of the liquid = 2xAρg

Using Newton’s 2^nd law,

ma = – 2xAρg

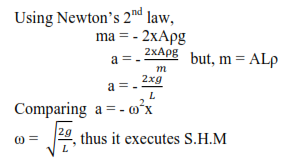
(ii) the oscillations eventually come to rest because energy is lost due to dissipative forces.

Example 9

(a)(i) What is meant by simple harmonic motion?

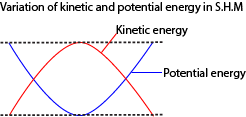
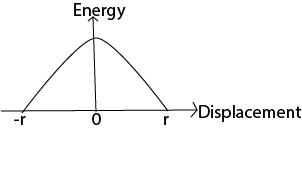
(ii) Show with a suitable sketch graph how the kinetic energy of a mass attached to the end of oscillating mass changes with distance from the equilibrium position.

(b) A mass of 1kg hangs from two springs S1 and S2 are connected in series as shown below. The force constant of the springs is 100N/m and 200N/m respectively.

Find

(i) the extension produced in the combination

(ii) the frequency of oscillation of the ass if it is pulled down a small distance and released.

(c) Explain with the aid of a sketch graph what would happen to the oscillations in (b)(ii) as the mass was immersed        in a liquid such as water.

Solution

(a) (i) It a special type of periodic motion in which the acceleration of the body along the path of the body is directed              towards a fixed point in the line of motion and is proportional to the displacement of the body from a fixed                    point.

(ii)

But v² = ω²(r²-x²)

K.E = mω²(r²-x²)

(b)(i) Considering spring S1

From Hooke’s law

mg = k₁x₁

1 x 9.81 = 100x₁

x₁ = 9.81 x 10^-2m

Similarly for spring S2

mg = k₁x₁

1 x 9.81 = 200x₁

x₁ = 4.905 x 10^-2m

Total extension = x₁ + x₂ = (9.81 + 4.905) x 10^-2m

= 1.4715 x 10^-1m

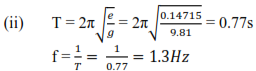
(b) If the mass is immersed in water, the amplitude decreases until the oscillations die away due to the loss of energy               arising from friction.

Example 10

(a) A mass of 0.1kg is suspended from a light spring of force constant 24.5Nm^-1. Calculate the potential energy of the mass.

(b) (i) State four characteristics of simple harmonic motion.

(ii) Show that the speed of a body moving with the simple harmonic motion of angular velocity, ω is given by v = ±ω  where, a, is the amplitude, and x, is the displacement from the equilibrium position.

(iii) Sketch graphs to show the variation with the displacement of kinetic and potential energies if a body moving with simple harmonic motion.

(c) A mass of 0.1kg suspended from a spring of force constant 24.5Nm^-1 is pulled vertically downwards through a              distance of 5.0cm and released. Find the

(i) Period of oscillation

(ii) Position of the mass 0.3 seconds after release.

 

Solution

Elastic potential energy

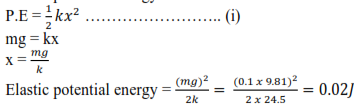
(b)(i)    The acceleration is directed towards a fixed point in a motion line

The acceleration is directly proportional to the displacement from a fixed point

It is periodic

Total mechanical energy is preserved.

(ii)

 

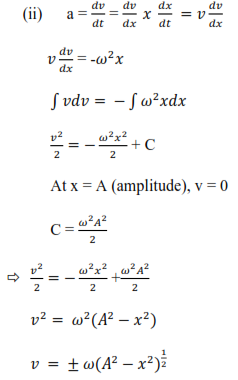
(iii)

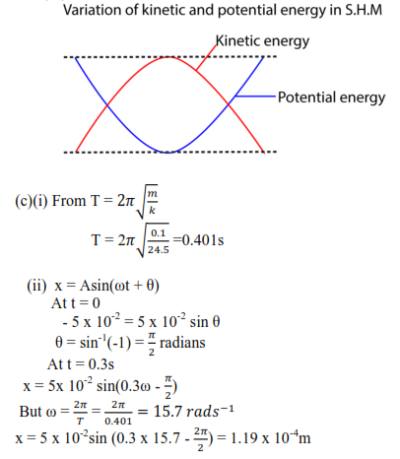
Example 11

(a) Defined simple harmonic motion.

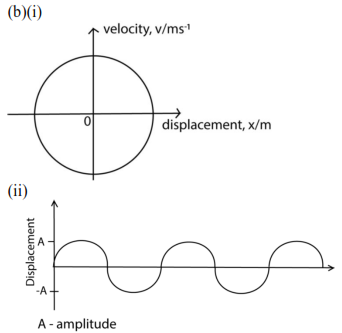
(b) Sketch the following graphs for a body performing simple harmonic motion

(i) Velocity against displacement

(ii) Displacement against time

(c) The period of oscillation of a conical pendulum is 2.0s. if the string makes an angle 60⁰ to the vertical at the                   point of suspension, calculate the

(i) Vertical length at the point of suspension above the circle.

(ii) Length of the string

(iii) The velocity of the mass attached to the string

(d) (i) Give an example of oscillating motion

(ii) What approximation is made in (b)(i)

Solution

(d)(i) simple pendulum

Liquid oscillating in a U-tube

Mass oscillating at the end of helical spring

(ii) the effect of the dissipative force is negligible.

Sponsored by The Science Foundation College + 256 753 80 27 09

Compiled by Dr. Bbosa Science