Surface tension

Common observation explained by surface tension

1.  A drop of water, on closing a tap remained dinging on the tap, as if the water was held in a bag.
2. A thin needle can be made to float on the surface as though it is denser than water
3. Mercury gathers in small spherical drops when poured on a smooth surface.
4. When a capillary tube is dipped in water, water is seen rising up in a tube
5. Insects can walk on the surface of the water
6. Rainwater forms beads on the surface of a waxy surface, such as a leaf. Water adheres weakly to wax and strongly to itself, so water clusters into drops. Surface tension gives them their near-spherical shape because a sphere has the smallest possible surface area to volume ratio.

All the above observation show that a liquid surface behaves as if it was or it is in a state of tension. The phenomenon is called surface tension.

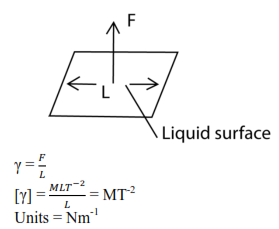
Surface Tension or Co-efficient of surface tension, γ

Is the force acting at right angle at one side of the imaginary line of length 1m drawn in the surface of a liquid.

Or

Surface tension is  an energy necessary to create a unit area of a surface under constant temperature, volume, and chemical potential.

Molecular theory of surface tension

The force F(r) between two molecules of a liquid varies with their separation r  as shown below

 

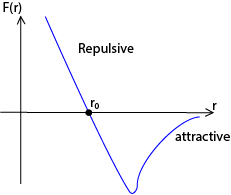
At the average equilibrium separation, r_o, F(r) = 0

For r> r₀ = the force is attractive to bring the distance between molecules to equilibrium separation, r₀.

For R < r₀ =the force is repulsive to restore the distance between molecules to equilibrium separation, r₀.

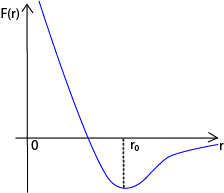
The corresponding potential energy variation with molecular separation, r, is shown below

 

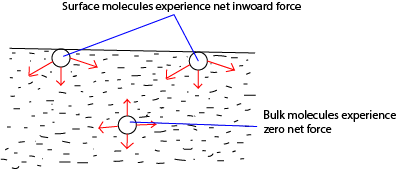
• The molecules within the body of the liquid (bulk) molecules are attracted equally by neighbors in all direction, hence, the force on the bulk molecules is zero, so the intermolecular separation for bulk molecules is r₀.
• For a surface molecules, there is a net inward force because there are no molecules above the surface to attract them equally.

 

• To the surface, work must be done against the inward attractive force, hence, a molecule in the surface of a liquid has greater potential energy than a molecule in the bulk. The potential energy stored in molecules at the surface is called free surface energy.

 

• Molecules at the surface their separation r > r₀. The attractive forces experienced by surface molecules due to their neighbors put in a state of tension and the liquid surface behave as a stretched skin.

Surface energy and shape of a drop of a liquid

System arrange themselves to achieve the least potential energy.

In liquids, the least potential energy is achieved by having the fewest number  molecules at the surface or by contraction of the liquid surface to the smallest possible area.

For this reason, free liquid drops are spherical because the spherical shape for any volume of a liquid gives the least surface area.

A large drop, however, due to its large weight flattens out in order to minimize the gravitational potential energy which tends to exceed the surface energy.

 

Factors affecting surface tension

1. Temperature lowers the surface tension of molecules because of molecules far apart and moving faster decreasing time to form temporary bonds.

A graph of surface tension against temperature

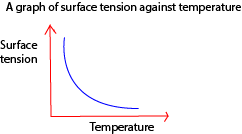
2. Impurities: these lower the surface tension forces because they displace molecules from their equilibrium positions and breaking bonds between them.
3. Detergent: reduce surface tension because they displace molecules from their equilibrium positions and break bond between them.

 

Angle of contact

This is the angle made between the solid surface and the tangent to the liquid surface at the point of intersection with the solid surface as measured through the liquid

 

A liquid makes an acute angle of contact with the solid surface when the adhesive force between  the liquid and the solid are greater than the cohesive forces between the liquid molecules themselves.

A liquid makes an obtuse  angle of contact with solid surface when the adhesive force between  the liquid and the solid are less than the cohesive forces between the liquid molecules themselves.

A liquid that makes an acute angle with the solid is said to wet the solid surface, for example, water wets glass. While a liquid that makes obtuse angle with the solid does not wet it, e.g. mercury does not wet glass but forms droplets on it.

The addition of detergents to water reduces the angle of contact and that is why it helps in washing.

The pressure difference in a bubble or curved surface

(a) Liquid curved surface

Consider a bubble formed inside a liquid as shown below

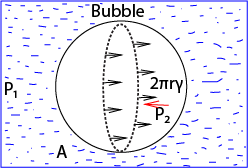
If we consider the equilibrium of one-half A,

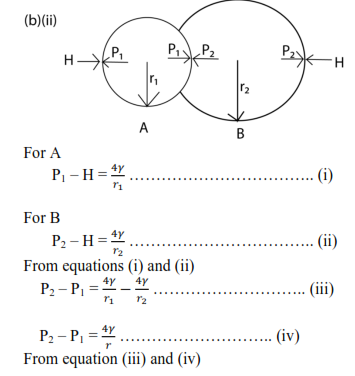
The force of tension on A plus the force on A due to external pressure P₁ = the force on A due to the internal pressure P₂inside the bubble

The force on A due to pressure P₁ = πr² x P₁ (where πr² is the area of circular face A

and since Pressure is force per unit area.)

the force on A due to pressure P₂ = πr² x P₂

 The surface tension force acts around the circumference of the bubble which has a length 2πr, thus the force = 2πrγ

It follow that:

2πrγ + πr² x P₁ = πr² x P₂

                                             2γ = r(P₂ – P₁)

Or P₂ – P₁) =

If p = (P₂ – P₁) , the excess pressure in the bubble over outside pressure

Then,  P =  ………………………………………………… (i)

The same formula for excess pressure holds for any curved liquid surface or meniscus, where r is its radius of curvature, and γ is its surface tension, provided the angle of contact is zero.

If the angle of contact is θ, the formula is modified by replacing γ by γcosθ.

Thus in general, excess pressure, P =  …………………………….. (ii)

 

(b) Excess pressure in a soap bubble

A soap bubble has two liquid surfaces in contact with air, one inside the bubble and the other outside the bubble.

The force on one half, A, of the bubble due to surfaces is thus = γ x 2πr x 2 = 4πrγ

For equilibrium of A, it follows that.

4πrγ + πr² x P₁ = πr² x P₂

Where P₂,and P₁ are pressure inside and outside the bubble respectively

Simplifying

P₂ – P₁ =

Therefore, excess pressure, P =   ………………………………………. (3)

 

Note that,

(i) the pressure on the concave side of the liquid is always greater than that on a convex side, e.g.

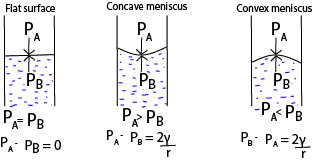
(ii) When the atmospheric pressure exceeds pressure inside the bubble, it collapses.

 

Capillary rise

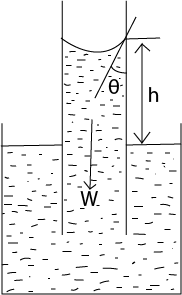
The liquid rises until the vertical component of the upward forces due to surface tension is equal to the weight of the liquid column.

Fγcosθ = W

γ =

F = γL

L = 2πr

But W = mg and m = Vρ (where ρ is the density of the liquid in kg/m³)

W = vρg = 2πr²hρg

Fγcosθ = 2πr²hρg

γ.2πrcosθ =2πr²hρg

h =

γ – coefficient of surface tension

θ – angle of contact

r – radius of capillary tube

ρ – density of the liquid

 

Example 1

A capillary tube is immersed in a liquid of density 13600kgm^-3 and the angle of contact is 140⁰. Find the capillary rise if the surface tension is 0.52Nm^-1 and a diameter of the tube is 0.32mm

the negative implies there was a capillary depression of 0.0096m

 

Example 2

(a) Define what is meant by surface tension in terms of surface energy.

(b) (i)Calculate the work done against surface tension in blowing a soap bubble of diameter 15mm if the surface tension of the soap bubble is 3 x 10^-2N/m

(ii) A soap bubble of radius r₁ is attached to another bubble of radius r₂. If r₁ is less than r₂, show that the radius of curvature of the common interface is

(c) (i) Sketch a graph of potential energy against the separation of two molecules in the liquid of a substance.

(ii) Explain the main features of the graph in(c)(i)

 

Solution

(a) Surface tension is the energy necessary to create a unit area of a surface under constant temperature, volume, and chemical potential.

(b) (i) Work done = surface tension x increase in surface area

Surface Area of a sphere = 4πr²

The soap bubble has two surface in contact with air, and thus it’s surface area = 4πr²

 

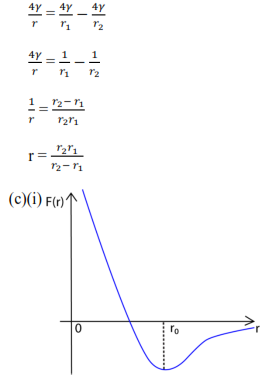
(c)(ii) At r = r₀, the resultant force is zero and the corresponding potential energy is minimum. So r₀ is the equilibrium separation

For r < r₀, the net force is repulsive, whereas r> r₀, the net force is attractive in order to restore the e separation to the equilibrium separation of r₀.

 

Example 3

(a) Define surface tension and derive its dimensions

(b) Explain using the molecular theory, the occurrence of surface tension

(c) Describe an experiment to measure the surface tension of a liquid by the capillary tube method.

(d) (i) Show that the excessive pressure in a soap bubble is given by P =

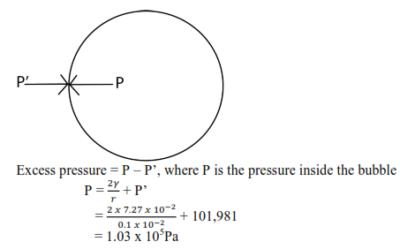
(ii) Calculate the total pressure within the bubble of air of radius 0.1mm in water if the bubble is formed 10cm below the water surface. And the surface tension of water is 7.27 x 10^-2N/m.(atmospheric pressure = 1.01 x 10⁵Pa)

Solution

Let the pressure at 10cm below the water surface be P’

Excess pressure = P – P’, where P is the pressure inside the bubble

Sponsored by The Science Foundation  College +256 753 80 27 09

Compiled by Dr. Bbosa Science