Heat Physic (A-level)

Heat

This is a form of energy which that rises the temperature of substances.

Means of heat transfer

1. Conduction

Conduction is the process of heat transfer through a substance from a region of high temperature to a region of low temperature without bulk movement of the medium; mainly by collision between atoms that vibrate about equilibrium positions

Mechanism of conduction

(a) Poor conductor

When one end of a poor conductor is heated, the atoms at the hot end vibrate with increased amplitude, collide with neighbouring atoms and lose energy to them. The neighbouring atoms also vibrate with increased amplitude, collide with adjacent atoms and lose energy to them. In this way, heat is transferred from one end to another.

Example 1

Explain how heat is conducted through a glass rod (3 marks)

Glass is a poor conductor therefore describe the mechanism of heat transfer in bad conductor.

(b) Good conductor

In good conductors heat is transferred from hot region to cold region by two mechanisms

• Good conductors contain free electron. When heated, the electrons at hot end gain more energy, move and transfer the energy to cold region by collision with atoms in solid lattice and other electrons.
• When one end of a good conductor is heated, the atoms at the hot end vibrate with increased amplitude, collide with neighbouring atoms and lose energy to them. The neighbouring atoms also vibrate with increased amplitude, collide with adjacent atoms and lose energy to them. In this way, heat is transferred from one end to another.

Because of the additional method of heat transfer by electrons, metals a better conductor of heat than insulators

Example 2

Explain the mechanism of heat transfer in metals (03marks)

Mechanism of heat transfer in good conductor required

Example 3

(i) Explain the mechanism of heat transfer in solids

The question requires description of conduction in both bad and good conductors

(ii) Why is a metal a better conductor of heat than glass?

Metals have additional mechanism of heat transfer by electrons.

 

2. Convections

Convection is a process of heat transfer in fluids from a region of high temperature to a region of low temperature, due to movement of the medium.

Mechanism of heat transfer by convection

When a fluid is heated from underneath, it expands and becomes less dense than fluid above. The warm less dense fluid rises to the top and the cool more dense fluid from above moves downwards to replace the rising fluid. This process continues and circulating current of the fluid is established until the whole fluid is heated up.

Example 4

(i) What is convection?

(ii) Explain how convection

3. Radiation

is a means of heat transfer through a vacuum or that does not involve a medium

 

Temperature

Temperature is the degree hotness or coldness.

The extent to which the body feels hot depends on the; average kinetic energy of the individual atoms or molecules with in that body. This means that the body’s kinetic energy is directly proportional to its thermal dynamic temperature.

Temperature is measured in degree Celsius, or Kelvin

Example 5

When is the temperature of 0K attained? (02marks)

Ok is when molecules of a substance slow down and attain their minimum total energy

Thermometry

This involves the study of thermometers as instruments used to measure temperature on the basis of certain physical thermometric properties which change with temperature and remains constant at constant temperature.

A thermometric property is a physical quantity which varies continuously, uniformly and linearly with temperature and remains constant at constant temperature.

 

Scales of temperature.

These are scales in which the measure of hotness or coldness of a body can be expressed .i.e. the measure of hotness or coldness of a particular body can be expressed in;

• Degrees centigrade (⁰C) forming a Celsius scale of temperature.
• Kelvin (K) forming a thermodynamic scale of temperature.
• Degrees Fahrenheit (⁰F) forming a Fahrenheit scale of temperature.

Conversion of scales

If t⁰C is temperature reading

Types of thermometers and thermometric property

Type of thermometers	Thermometric property
Liquid in glass	Length of liquid column
Electrical resistance thermometer e.g. platinum resistance	Resistance of the platinum wire
Gas thermometer e.g. constant volume gas thermometer	Changes in pressure with temperature
Thermocouple	Induced e.m.f
Radiation pyrometer	Radiation

Qualities of a good thermometric property

• Considerably vary for small changes in temperature.
• Vary over a wide range of temperature (both high and low)
• Vary linearly, uniformly and continuously with temperature
• Be accurately measurable over a wide range of temperature with a simple apparatus

Related concepts

• Fixed point is defined as constant temperature at which a physical state of pure water is expected to change at 760mmHg. Fixed points are basically two i.e. 0⁰C and 100⁰
• Lower fixed point (T₀) is the temperature of pure melting ice at 760 mmHg. It is 0⁰
• Upper fixed point (T₁₀₀) is the temperature of pure steam at 760mmHg. It is 100⁰
• Triple point (T_tr) is the temperature at which pure water pure steam and pure ice co – exist in equilibrium at 760mmHg. It is 0.16⁰ C or 273.16K.
• Fundamental interval is the range of the thermometer readings at the two fixed points e.g. for thermometers which give direct readings of temperature = 100⁰

  

Establishing scales of temperature

• Chose a physical property of substance (X)
• Determine the value of the property at the upper fixed point of the thermometer (X₁₀₀). This is done by placing the bulb of the thermometer in steam at 760mmHG until a constant reading is obtained.
• Determine the value of the property at the upper fixed point of the thermometer (X₀). This is done by placing the bulb of the thermometer in melting ice at 760mmHG until a constant reading is obtained.
• If the value of the thermometric property at temperature, θ, is X_θ.

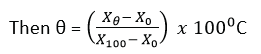
Thermal dynamic scale of temperature

On this scale of temperature is measured in “Kelvin” or K and makes use of triple point only.

If X_tr is the value of a thermometric property at the triple point and X_T is the value of thermometric property at temperature,

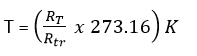
Using a platinum resistance thermometer

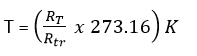
Where

• R_T is the resistance of the wire at unknown temperature, T.
• R_tr is the resistance of the wire at the triple point of water.

Example 6

The pressure recorded by a constant volume gas thermometer at temperature T is 4.8 x 10⁴Nm^-2. Find T if the pressure at the triple point of water is 4.2 x 10⁴Nm^-2.

Solution

Absolute zero temperature

This is the temperature of an ideal gas which corresponds to its zero volume or zero pressure it exerts on the walls of the container in which it is trapped. This value approximates to the triple point of pure water i.e. – 273⁰C or 0K.

Molecular explanation for existence of absolute zero temperature

When a gas is cooled, its molecules loose kinetic energy continuously since it depends directly on temperature. As molecules loose kinetic energy they move closer into close proximity until when they cease to have kinetic energy. At this point the gas is said to occupy a negligible volume and its temperature at this point is called the absolute zero temperature and the pressure the gas exerts on the walls of the container occupied is negligible.

Estimating absolute zero temperature

• Volumes a fixed mass of a gas at various temperatures are determined.
• The volumes of the gas are plotted against corresponding temperature.

Absolute zero temperature is determined by extrapolating the graph until when it touches the temperature axis and is found to be -273⁰C or 0K.

Types of thermometers

1. Liquid in glass thermometer

Depends on expansion of the liquid

Advantages of liquid-in-glass thermometer.

• The thermometer is simple, cheap and portable.
• The thermometer can be calibrated to give direct readings e.g. clinical thermometer

Liquids used in thermometers

Mercury

Advantages

• withstands high temperature without change of state
• does not wet glass
• expands uniformly

Disadvantage

• it is expensive
• it is poisonous

Alcohol

Advantage

• Measures low temperatures because of its low freezing point
• Cheap

Disadvantages

• does not measure high temperature above 78⁰
• wets glass
• Water is not used because it has irregular expansion
• Cannot measure temperatures below 0⁰Cor above 100⁰C

 

2. Constant volume gas thermometer

• Place the bulb inside an enclosure whose temperature is to be measured.
• Allow some time for the gas to acquire the temperature of the enclosure. The gas in the bulb may expand and forces mercury up the adjustable tube.
• Adjust the adjustable limb to bring back mercury to constant volume at A and record the height of mercury, h_θ.
• The Celsius scale is given by

where h₁₀₀ and h₀ are the heights at steam and ice points

Limitations

• The temperature of the gas in the dead space is different from that of the gas in the bulb
• Thermal expansion of the bulb may lead to change in volume
• Capillary effect on the mercury surface.

Correction

• The dead space should be made small
• The bulb should be made of material with low thermal expansivity
• The manometer tubes should be widened and with the same diameters.

Advantages of constant volume gas thermometers.

• It is very sensitive since a small change in temperature leads to a great expansion of a gas
• Gas thermometers give accurate results since pressure vary linearly with temperature
• Can measure wide range of temperature.

Disadvantages of constant volume gas thermometers

• it is bulky and delicate
• does not give direct readings
• it cannot measure temperature at a point
• it does not measure rapidly changing temperature

Example 7

Value of property
Pressure in mmHg	Ice point	Steam point	Room  temperature
	760	1040	795

(i) Using the above data, calculate the room temperature on the scale of the constant volume gas thermometer.

(ii) Explain why a gas thermometer is seldom used for temperature measurements in a laboratory.

• it is bulky and delicate
• does not give direct readings
• it cannot measure temperature at a point
• it does not measure rapidly changing temperature

3. Resistance thermometer

• Place the resistance thermometer in a funnel with crushed ice and leave it for some time.
• Close the switch and obtain a balance point by adjusting the resistance box,
• Determine the resistance R₀ at 0⁰C from

• Transfer the resistance thermometer a beaker containing boiling water and after some time, determine resistance R₁₀₀.
• Place the resistance thermometer in water at room temperature and determine resistance R_θ.
• Temperature of the room temperature,

Advantages

• It is accurate
• Has fairly wide range of temperature

Disadvantages

• Cannot measure temperature at a point
• It cannot be used to follow rapidly changing temperatures

Example 8

The resistance of a certain platinum resistance thermometer is found to be 2.56Ω at 0⁰C, 3.56Ω at 100⁰C and 6.78Ω at 444.5⁰C, the boiling point of sulphur on the gas scale

(a) Calculate boiling point of sulphur on the platinum resistance scale.

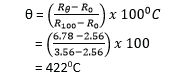
(b) Why are the two values of boiling point of sulphur differ

Different thermometric properties in different thermometers vary differently with temperatures

4. Thermocouples

It consists of different metals such as copper and iron joined in a circuit and their junctions kept at different temperatures. This causes a small current to be produced

Mode of action

• The cold junction is put in water at 0⁰C and e.m.f, E₀ is determined.
• The other junction is put at a point whose temperature is required
• As a result of difference in temperature, a thermal e.m.f and causes a deflection of the galvanometer, E_θ.
• The hot junction is placed at steam point and e.m.f, E₁₀₀ is determined

Advantages of a thermocouple

• Can be used to measure temperature at a point
• Can measure rapidly changing temperature
• Can give direct readings
• Has wide range

Disadvantages of a thermocouple

• Not accurate
• Two values of temperature θ1 and θ2 may correspond to one e.m.f.

5. Pyrometers

A pyrometer is a thermometer used to measure very high temperatures by using the radiation that the body emits and wavelength of the radiation as the thermometric property.

Optical pyrometer

Mode of action

• the filament is focused on the eye piece and the objective focuses the object so that the image of the object lies in the same plane as the filament
• Light from the hot object and the filament is passed through the red filter and viewed by the eyepiece.
• Current is adjusted by the rheostat R until the filament and the object are equally bright.
• The temperature of the hot body is then read from the calibrated ammeter, A.

 

 Calorimetry

Thermal equilibrium

This is a state of the body in which there is no net flow or exchange of heat within it or between it and its surroundings.

The Zeroth law of thermodynamic

It states that if two bodies are each in thermal equilibrium with a third body, then all the three bodies are in thermal equilibrium with each other.

The principle of conservation of energy

The principle of conservation of energy can be expressed mathematically by the equation

ΔQ = ΔU + ΔW

Where

ΔQ is the quantity of heat given to the system

ΔU is the rise in internal energy, the rise in internal energy is indicated by the rise in temperature

ΔW is the external work done by the system such as expansion against atmospheric pressure.

Heat capacity

This is the quantity of heat required to raise the temperature of the body by 1⁰C or 1K.

It follows that if the temperature of a body whose heat capacity C rises by Δθ when the amount of heat ΔQ is added to it

ΔQ = CΔθ ………………………. (i)

Specific heat capacity  (s.h.c), c

This is the amount of heat required to raise the temperature of 1kg mass of a substance through 1⁰C or 1K.

It follows that if the temperature of a body of mass m and s.h.c, c rises by Δθ when an amount of heat ΔQ is added it, then

ΔQ =mcΔθ …………………… (ii)

From (i) and (ii)

C = cm

Molar heat capacity

This is the heat required to raise the temperature of 1 mole of a substance by 1Kor 1⁰C.

Units: Jmol^–1K^-1

Measurement of specific heat capacity

(a) Measurement of specific heat capacity of solid/metal (copper, and aluminium ) that are good conductors using electrical method

• Two holes are drilled into the specimen solid of mass m.
• A thermometer is inserted in one of the holes and an electric heater into the other hole. The holes are then filled with a good conducting fluid, e.g. oil to ensure thermal contact.
• The apparatus is insulated and initial temperature θ₀ is recorded.
• The heater is switched on at the same time a stop clock is started.
• The steady values of ammeter reading, I and voltmeter reading, V are recorded.
• After considerable temperature rise, the heater is switched off and stop clock stopped.
• The highest temperature θ₁ recorded and time t taken noted.
• Assuming negligible heat loss, the specific heat capacity, c, of the conducting solid is calculated from

Precautions

• The block of metal should be highly polished and heavily lagged.
• The two holes should be filled with either mercury or light oil to improve thermal contact with the heater and thermometer.

 

(b) Measurement of specific heat capacity of a liquid by electrical method

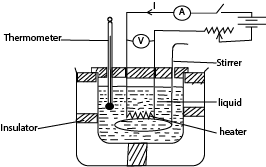
• A liquid of known mass, m is poured in a double walled calorimeter of a known heat capacity, C
• The setup is as shown above
• The initial temperature θ₁ of the liquid and calorimeter is recorded.
• Switch K is closed and simultaneously a top clock is started.
• The ammeter and voltmeter readings I and V are respectively recorded.
• The liquid is stirred as it is heated, and after sometime, t of heating, the current is switched off and final temperature θ₂
• Assuming no heat loss; heat supplied by the heater = heat received by water and calorimeter

i.e. IVt = (mc + C)(θ₂ – θ₁), where c is the specific heat capacity of a liquid.

 

(c) Measurement of specific heat capacity of a liquid by continuous flow method

• A liquid is allowed to flow at constant rate
• Power is switched on and the liquid is heated until temperatures registered by T₁ and T₂ are steady and the values θ₁ and θ₂ respectively are recorded.
• The p.d V and current I are recorded from the voltmeter and ammeter respectively
• The mass, m of a liquid collected in time t is recorded
• At steady state; VIt = mc(θ₂ – θ₁) + h ………….. (i)

where h is heat lost to the surrounding

• The rate of flow is changed and the voltage and current are adjusted until the steady readings of T₁ and T₂ are θ₁ and θ₂ respectively
• If m₁, V₁ and I₁ are the values mass of liquid collected in time t, voltmeter and ammeter readings respectively, then

V₁I₁t = m₁c(θ₂ – θ₁) + h ………….. (ii)

Subtracting (ii) from (i)

Example 9

In a continuous flow experiment, a steady difference of temperature of 1.5⁰C is maintained when the rate of liquid flow is 4.5gs^-1 and the rate of electrical heating is 60.5W. On reducing the liquid flow rate to 1.5gs^-1, 36.5W is required to maintain the same temperature difference.

Calculate the

(a) Specific heat capacity of the liquid. (04marks)

P = cθ + h

60.5 = 4.5 x 10^-3 x c x 1.5 + h ………… (i)

36.5 = 1.5 x 10^-3 x c x 1.5 + h ………… (ii)

Subtracting (ii) from (i)

24 = 3 x x 10^-3 x c x 1.5

c = 5,333Jkg

(b) Rate of heat loss to the surroundings (03marks)

Substituting c in (i)

60.5 = 4.5 x 10^-3 x 5333 x 1.5 + h

h  = 24.5W

(d) Measurement of specific heat capacity of a solid by the method of mixtures

• A solid on mass m_s kg and specific heat capacity, c_s, is heated in boiling water at temperature at temperature θ₁⁰C and quickly transferred to a calorimeter of heat capacity, C, containing water of mass, m₁ and , at the temperature θ₂.
• The final constant temperature θ₃ of the mixture is determined.

        Assuming there is no heat loss

Heat lost by the solid = heat gained by calorimeter + heat gained by water

m_s x c_s x (– θ₃) = (C + m₁)(θ₃ – θ₂)

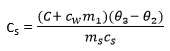
where c_w is specific heat capacity of water

 

Precautions

• The calorimeter must be heavily lagged.

(e) Measurement of specific heat capacity of a liquid by the method of mixtures

• A solid on mass m_s kg and specific heat capacity, c_s, is heated in boiling water at temperature at temperature θ₁⁰C and quickly transferred to a calorimeter of heat capacity, C, containing a liquid of mass, m₁ and , at the temperature θ₂.
• The final constant temperature θ₃ of the mixture is determined.

Assuming there is no heat loss

Heat lost by the solid = heat gained by calorimeter + heat gained by water

Precautions

The calorimeter must be heavily lagged.

Example 10

Apiece of copper of mass 100g is heated to 100⁰C and then transferred to a well-lagged copper can of mass 50g containing 200g of water at 10⁰C. Neglecting heat loss, calculate the final steady temperature of the of the mixture.

[Specific heat capacity of copper and water are 400Jkg^-1K^-1 and 4200Jkg^-1K^-1)

Solution

Let the final temperature be θ.

Heat lost by the copper mass = heat gained by the copper can + heat gained by water

0.1 x 400 x (100 – θ) = 0.05 x 400 x (θ – 10) + 0.2 x 4200 x (θ – 10)

θ = 14.0⁰C

Example 11

(a) State two advantages of the continuous flow method over the method of mixtures. (01mark)

• No cooling correction is required
• Heat capacity of the apparatus is not requires
• Temperature measured at leisure when steady
• Resistance of the heater not required

 

(b) State two disadvantages of the method in (c)(i) (01mark)

• larger volumes of liquid required
• not suitable for volatile liquids.

 

Newton’s law of cooling

Newton’s law of cooling states that under forced convection, the rate of loss of heat of a body is directly proportional to its excess temperature over that of the surrounding.

The rate of heat loss also depends on

• Surface area of the body and,
• Nature of the surface, i.e. whether dull or shiny

Hence for a body of a uniform temperature, θ and surface area A

NB. A small body cools faster than a big body because a small body has a larger surface area to volume ration.

An experiment to verify Newton’s law of cooling.

• Hot water is placed in a calorimeter that is standing on an insulating surface and is put in a draught.
• The temperature, θ, of the water is recorded at suitable intervals.
• The room temperature θ_R is recorded.
• Plot a graph of temperature against time to get a graph similar to the one below.

• Draw tangent at various temperatures, θ and obtain their slopes. These slopes give the rate of temperature fall.
• Plot these slopes with corresponding excess temperatures (θ – θ_R)
• A straight line graph is obtained implying that the rate of heat loss is proportional to excess temperature.

 

Example 12

Describe an experiment to verify Newton’s law of cooling. (05marks)

 

Cooling correction

Despite all precautions to prevent heat losses in experiments of the mixtures, still there will be some significant heat loss that will prevent the mixture to attain maximum temperature rise. An estimate has to be made of the temperature that would have been attained if these heat losses were not there. The small temperature added to the observed maximum temperature to make up for the heat lost to the surrounding during the experiment is called cooling correction.

 

Definition of cooling correction

This is the extra temperature difference to be added to the observed maximum temperature of the mixture to make up for the heat lost to the surrounding during the experiment.

 

Experiment to determined cooling correction

• Pour a liquid in a calorimeter and place it on a table
• Place a thermometer into the liquid and after sometime, record the temperature of the surroundings, θ₀.
• Gently place a hot solid into the liquid and stir.
• Record the temperature of the mixture at suitable interval until the temperature of the mixture has fallen by about 1⁰C below the observed maximum temperature, θ₁.
• Plot a graph of temperature against time

• The broken line shows how we would expect the temperature to rise if no heat were lost and the difference, P, between the plateau of this imaginary curve, and the crest of the experimental curve, E. is known as the ‘cooling correction’
• Draw a line AC through θ₀ parallel to the time axis.
• Draw a line BE through θ₁ parallel to the temperature axis.
• Draw a line CD beyond BE parallel to the temperature axis and note Δθ
• Estimate the area A₁ and A₂ under the graph by counting the square on the graph paper
• Cooling correction, P s given by the graph

Cooling correction,

Example 13

(i) What is meant by cooling correction? (01marks)

This is the extra temperature difference to be added to the observed maximum temperature of the mixture to make up for the heat lost to the surrounding during the experiment.

(ii) Explain how the cooling correction may be estimated in the determination of the heat capacity           of poor by the method of mixtures (05marks)

 

Latent heat

Definition

This is the quantity of heat absorbed or released when a substance changes physical state at constant temperature. E.g. during melting, evaporation, sublimation, condensing, solidification

Example 14

Explain why there is no change in temperature when a substance is melting (04marks)

Supply of heat to a melting solid reduces the forces of attraction between the molecules and increases the separation between them. This increases the potential energy (P.E) between the molecules while keeping kinetic energy (K.E) of the molecules the same. Further increase in separation between the molecules causes the regular pattern to collapse as the solid changes to liquid. Until this process is complete, the temperature does not change.

Example 15

Explain the changes that take place in the molecular structure of substances during fusion and evaporation (04marks)

Heat supplied during fusion breaks down the forces that keep ordered pattern of molecules is solid crystalline structure to form a liquid. The potential energy of the molecules increase but the average kinetic energy and temperature of the molecules remain unchanged.

Heat supplied during evaporation breaks molecular bonds in liquids and allow gas molecules to expand against atmospheric pressure which allows then to move independently.

Example 16

Explain why the specific latent heat of evaporation is always greater than specific latent heat of fusion of a substance at the same pressure are different. (04marks)

Change from solid to liquid, intermolecular bonds are weakened and there is a small increase in volume. This implies there negligible change in volume and thus little work done against atmospheric pressure.

During vaporization, a lot of heat is required to break molecular bonds in a liquid and to enable expansion to larger volume of a gas against atmospheric pressure.

 

Specific latent heat of fusion

Specific latent het of fusion is the amount of heat required to change 1kg mass of a substance from solid to liquid without change of temperature. Units are Jkg-1

Experiment to determine the specific latent heat of fusion by the method of mixtures

• A known mass m₁ kg of water at temperature θ₁ (a few degrees above room temperature) is placed in a calorimeter of mass m_c kg and heat capacity. C.
• A small piece of dry ice (dried by blotting paper) is added to the water and stirred to a constant temperature θ₂.
• The total mass, m, of the calorimeter and water and ice is determined.

Calculation

Mass of ice = (m – (m₁ + m_c) = m₃kg

Heat lost by water and calorimeter = heat gained by ice to melt and again temperature to θ₂.

Suppose c and l_f are the specific heat capacity and latent heat of fusion of water, then

(m₁c + )(θ₁ – θ₂) = m₃l_f + m₃c(θ₂ – 0)

Experiment to determine the specific latent heat of fusion by electrical method

• Place pure ice in a funnel such that it submerge the heater
• With R set, close K and simultaneously start a stop clock.
• Collect a known mass m of water in a specified time, t.
• Record the readings I and V of the ammeter and voltmeter spectively.

Assuming no heat gain from the surrounding

Heat supplied by the heater = heat gained by ice.

IVt -= ml_fb where  l_f is the specific latent heat of fusion

NB: if heat lost gained from the surrounding is h

Then IVt + h = mlf ………………….. (i)

The experiment is repeated  for different values of V’, I’ and m’ in the same time

I’V’t + h = m’lf ………………….. (ii)

Combining (i) and (ii)

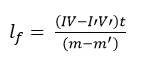
Specific latent heat of vaporization

Specific latent het of vaporization is the amount of heat required to change 1kg mass of a substance from liquid to vapour without change of temperature. Units are Jkg-1

Experiment to determine the specific latent heat of vaporization of water by electrical method

• Put the liquid whose specific latent heat of vaporization is required in a vacuum jacketed vessel as shown above.
• The liquid is heated to boiling point.
• The current, I, and voltage, V are recorded.
• The mass of condensed water, m, condensed in time, t, is determined.
• Then

where h is the rate of heat loss to the surroundings

• To eliminate, h, the experiment is repeated for different values of I’ and V’ and the mass of the condensed water, m’ condensed in tie t is determined.

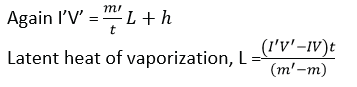
Example 17        

An appliance rated 240V, 200W evaporates 20g of water in 5 minutes. Find the heat loss if specific latent heat of vaporization is 2.26 x 10⁶Jkg^-1. (03marks)

Electrical energy supplied = mlv + h

Power x time = mlv + h

200 x 5 x 60 = 20 x 10^-3 x 2.26 x 10⁶ + h

h = 14800J

An experiment to determine the specific latent heat of vaporization of water by the method of the mixtures 

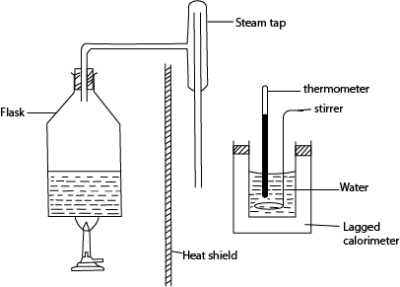
• The initial temperature θ₀ and mass, m of water in the calorimeter are measured
• Steam from boiling water is passed into water in a calorimeter and after a reasonable temperature rise, flow of steam is stopped and final temperature, θ_f is recorded.
• Mass m₂ of water in the calorimeter is then taken
• The mass of steam condensed, m_s = (m₂– m)

Given that the heat capacity of the calorimeter= C

Heat gained by steam = heat gained by water and calorimeter

m_sc_v + m_sc(100- θ_f) = (m₂ – m)c(θ_f – θ₀) + C(θ_f – θ₀)

c_v = specific latent heat of vaporization

c= specific heat capacity of water

Example 18

Explain why evaporation causes cooling? (03marks)

When a liquid evaporate molecules with high kinetic energy escape leaving molecules with low kinetic energy. Since temperature of the liquid depends on the average kinetic energy of its molecules, the temperature drops.

Example 19

Explain the effect of pressure on the boiling point of a liquid. (02marks)

• Since a liquid boils when its saturated vapour pressure  is equal to external pressure.
• Increasing the external pressure increases the boiling point of a liquid because the liquid has to be heated to a higher temperature to make its saturated vapour pressure equal to external pressure

 

 Gas laws and heat capacity

Gases

Definition

A gas is a term applied to a substance which is in the gaseous phase above its critical temperature.

A critical temperature is a temperature above which a gas cannot be liquefied no matter how great the pressure is.

Gas laws

(a) Boyle’s law

States that the pressure of a fixed mass of a gas is inversely proportional to volume. If P stand for pressure and V for volume; then

In general. When the pressure and volume of a gas change from P₁ and V₁to P₂ and V₂ respectively at constant temperature, then P₁V₁ =P₂V₂.

 

An experiment that can be used to verify Boyles’ law.

• air in the closed limb of a U-tube barometer as shown above
• mercury is poured to a height, h, and the length of the air column, L is noted.
• the length h is varied to obtain different sets of values of h and L
• Pressure of the gas is calculated from P = (H + h)ρg where H= height of barometer corresponding to atmospheric pressure, ρ = density of mercury, g = acceleration due to gravity. Note that h can be positive or negative.
• If A is the cross section area, V =AL
• Values of h, L, P, V and 1/V are tabulated
• A plot of P against 1/V gives a straight line through the origin which verifies Boyle’s law.

 

(b) Charles’ law

Charles’s states that the volume of a fixed mass of a gas is directly proportional to its absolute temperature at constant pressure

A graph of volume against temperature is shown below

In general when the volume and temperature of a gas change from V1 and T1 to V2 and T2 respectively at constant pressure, then,

Experiment to verity Charles’ law

• Dry air is trapped in the closed limb as shown above
• The level of mercury in the two limbs is maintained at the same level by adding or removing mercury at each temperature of the bath to ensure that pressure of the air is equal to atmospheric temperature.
• The length L of the air column and temperature of the water bath θ are recorded.
• Several values of L and θ are obtained by passing steam
• A graph of L against θ gives a straight line showing that the volume of the gas is proportional to temperature.

(c) Pressure law

It states that the pressure of a fixed mass of a gas is proportional to temperature provided the volume is constant. i.e.

Ideal gas equation or equation of state

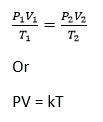
Example 20

A gas cylinder has volume of 0.040m³ and contains air at pressure of 2.0MPa. Assuming that the temperature remain constant, calculate

(a) The equivalent volume of air at atmospheric pressure of 1.0 x 10⁵Pa

From PV = constant

0.04 x 2 x 10⁶ = V x 1.0 x 10⁵

V= 0.8m³

 

(b) The volume of air, at atmospheric pressure, which escapes from the cylinder when it is opened to atmosphere.

0.8 -0.04 = 0.76m³

i.e. air escapes from the cylinder until it contains 0.04m³ of air at atmospheric pressure

 

(d) Dalton’s law of partial pressures

States that the total pressure of a mixture of gases, which do not react chemically is equal to the sum of the partial pressures of the gas.

Example 21

Two cylinders A and B of volumes V and 3V respectively are separately filled with a gas. The cylinders are connected as shown above with the tap closed. The pressures of A and B are P and 4P respectively. When the tap is opened the common pressure becomes 60Pa. Assuming isothermal conditions find the value of P. (04marks)

Solution

External work done by expanding gas.

Suppose the gas expands by dv so that the piston moves out through a small distance dx.

Work done by the gas, dW = Fdx

= PAdx

= Pdv

Total work done during expansion from v₁ to v₂ is given by

Example 22

When 1.5kg of water is converted to steam at (100⁰C) at standard pressure (1.01 x 10⁵Nm^-2) 3.39MJ of heat is required. During the transformation from liquid to vapour, the increase in volume of water is 2.5m³.

(i) Calculate the work done against the external pressure during the process of evaporation.

From ΔW = P(V₂ – V₁)

External work done = 1.01 x 10⁵ x 2.5 = 2.53 x 10⁵J

(ii) Explain what happens to the rest of the energy.

The difference in energy is the increase in internal energy of water molecules.

i.e. 3.39 x 10⁶ – 2.53 x 10⁵ = 3.24 x 10⁶J = increase in internal energy of water molecules.

 

Molar Heat capacities

Definition

Molar heat capacity of a substance is the amount of heat required to raise the temperature of one mole of it by 1K. It is expressed in Jmol^-1K^-1.

Molar heat capacity at constant volume, c_v

Molar heat capacity at constant volume of a substance is the amount of heat required to raise the temperature of one mole of it by 1K at constant volume. It is expressed in Jmol^-1K^-1.

Molar heat capacity at constant pressure, c_p

Molar heat capacity at constant pressure of a substance is the amount of heat required to raise the temperature of one mole of it by 1K at constant pressure. It is expressed in Jmol^-1K^-1.

 

The relationship between the principal molar heat capacities C_p and C_v for an deal gas. (05marks)

From dQ = dU + dW……………. (i)

But dQ = C_pdT, dU = C_vdT and dW= PdV = RdT

Substituting in (i)

C_pdT = C_vdT + RdT

C_p – C_v = R

Where R is the universal gas constant per unit mass.

Example 23

The temperature of 1mole of helium gas at a pressure of 1.0 x 10⁵Pa increases from 20⁰C to 100⁰C when the gas is compressed adiabatically.

Find the final pressure of the gas. (Take C_p/C_{v =} γ =1.67) (04 marks)

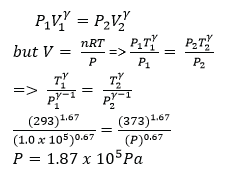
Example 24

Nitrogen gas is trapped in a container by a movable piston. If the temperature of the gas is raised from 0⁰C to 50⁰C at constant pressure of 4.0 x 10⁵Pa and the total heat added is 3.0 x 10⁴J, calculate the work done by the gas. [The molar heat capacity of nitrogen at constant pressure is 29.1Jmol^-1K^-1, C_p/C_v= 1.4]

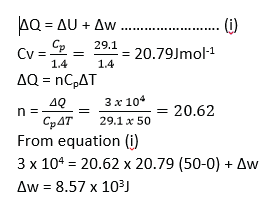
Example 25

Ten moles of a gas, initially at 27⁰C are heated at constant pressure of 1.01 x 10⁵Pa and volume increased from 0.25m³ to 0.375m³. Calculate the increase in internal energy.

[Assume C_p = 28.5Jmol^-1K^-1] (06marks)

Example 26

An ideal gas at 18⁰C is compressed adiabatically until the volume is halved. Calculate the final temperature of the gas. [Assume specific heat capacities of the gas at constant pressure and volume are 2100Jkg^-1K^-1 and 1500Jkg^-1K^-1] respectively. (04marks)

Dalton’s Law

Dalton’s law states that the total pressure of a mixture of gases which do not interact chemically is equal to the sum of partial pressures of the individual gases.

Definition

Partial pressure is the pressure of an individual gas in a mixture or partial pressure of a gas in a mixture is the pressure which it would exert if it were allowed to occupy the volume of the mixture at the same temperature as the mixture

 

The kinetic theory of matter.

• Gases are composed of molecules which are in continuous random motion.
• The molecules collide elastically with one another and also with the walls of the container.
• The pressure of a gas is due to the molecules bombarding the walls of its container. Whenever a molecule bounces off a wall, its momentum at right-angles to the wall is reversed; the force which it exerts on the wall is equal to the rate of change of its momentum. The average force exerted by the gas on the whole of its container is the average rate at which the momentum of its molecules is changed by collision with the walls.

 

Calculation of pressure

To find the pressure of the gas we must find this force, and then divide it by the area of the walls.

Assumptions

• The attraction between the molecules is negligible.
• The volume of the molecules is negligible compared with the volume occupied by the gas.
• The molecules are like perfectly elastic spheres.
• The duration of a collision is negligible compared with the time between collisions.

Consider a molecule of mass, m, moving in a cube of length, l and velocity, u.

Definition

Mean square speed is the average square speed of the gas molecules at a particular temperature, T

Root-mean-square speed, is the square root of mean of square velocities of gas molecules.

Therefore, the average kinetic energy of translation of the random motion of the molecule of a gas is proportion to the kinetic energy.

 

Example 27

If the mass of 1mole of hydrogen is 2.0g and this occupies a volume of 0.022m3 at 273K and pressure of 105Nm-2. Calculate the r.m.s speed of hydrogen at 546K.

 

Example 28

Derive the expression P =  for the pressure, P, of an ideal gas of density ρ and mean square speed, . State any assumptions made (07marks)

Example 29

Example 30

Explain why the pressure of a fixed mass of a gas rises if its temperature is increased. (02marks)

When the temperature of a fixed mass of a gas is increased, at constant volume, the velocities and kinetic energy of molecules is increased. They bombard the walls of the container more frequently with increased force. This increases pressure since pressure is proportional to force.

Example 31

Explain the following observations using the kinetic theory.

(i) A gas fills any container in which is it placed and exerts pressure on its walls. (03marks)

A gas contains molecules with negligible intermolecular forces and free to move in all directions. As they move, they collide with each other and with the walls of the container. The unrestricted movements make them to fill the available space and collisions with the walls contributes to the pressure exerted on the wall.

(ii) The pressure of a fixed mass of a gas rises when temperature is increased at constant volume. (02 marks)

When the temperature of a gas increases, the kinetic energy of the gas molecules increases. This increases the frequency and force of collision against the wall leading to increase in pressure.

Example 32

Explain why the pressure of a fixed mass of a gas in a closed container increases when the temperature of the container is raised. (02marks)

When the temperature of the container increases, the average velocity of the molecules increases.  So the number and force of collisions with the walls of the container per second increases. Consequently the momentum change per second increases as they bombard the walls. This leads to increase in the impulsive force exerted on the walls causing increase in pressure

 

Graham’s law

States that the rate of diffusion of a gas is inversely proportional to the square root of its density.

At the same Kelvin temperature T, the mean kinetic energies of the molecules of different gases are equal.

If subscript 1 and 2 denote gases 1 and 2 respectively

At a given temperature and pressure, the density of a gas, ρ, is proportional to the mass of its molecule, m, since equal volumes contain equal number of molecules

The equation

• shows that the average molecular speeds are inversely proportional to the square roots of the densities of the gases.
• explains why the rates of diffusion-which depend on the molecular speeds-are also inversely proportional to the square roots of the densities.

 

Real gases

As opposed to ideal gases, in real gas;

• The volume of the molecules may not be negligible in relation to the volume V occupied by the gas.
• The attractive forces between the molecules may not be negligible.

 Real gas equation

To account for molecular volume and intermolecular forces J.H. Vander Waal proposed the following equation

For 1mole of a gas

corrects deficit in pressure due to intermolecular attractions of gas molecules and

b, called the co-volume accounts for the finite volume of molecules themselves

NB:  (i) A real gas obeys ideal gas equation above the critical temperature

Differences between ideal and real gases

• Ideal gases obey Boyle’s law while real gases do not.
• The volume of the molecules of ideal gases are negligible compared to the container while for the real gases the volume is not negligible.
• Ideal gases have negligible intermolecular forces while the intermolecular forces of real gases are not negligible
• The velocity of ideal gas molecules is constant in between collision while real gases molecules do not have constant velocity due to intermolecular forces.

 

Vapours

A gas is the gaseous state of a substance above its critical temperature, T_C.

A vapour is the gaseous state of a substance below its critical temperature.

A graph of a real gas below and above the critical temperature

• Above the critical temperature a gas obeys Boyle’s law.
• Below the critical temperature a gas exist as unsaturated vapour at low pressure when the pressure is increase it condenses until all the gas is turned into a liquid.

A critical temperature is a temperature above which a gas cannot be turned into a liquid by compression.

 

Saturated and unsaturated vapour

Unsaturated vapour is a vapour that is not in dynamic equilibrium with its own liquid while saturated vapour is a vapour that is in dynamic equilibrium with its own liquid

Differences between saturated and unsaturated vapours.

• A saturated vapour pressure is one which is in dynamic equilibrium with its own liquid and an unsaturated vapour is one that is not in dynamic equilibrium with its own liquid.
• A saturate vapour pressure does not obey gas laws whereas unsaturated vapour approximately obey gas laws.

Sketches of graphs of pressure against temperature for an ideal gas and for saturated water vapour originally at 0⁰C

 

An experiment to determine saturated vapour pressure at a given temperature.

• The pressure of the air in R is shown by the mercury manometer; if its height is h, the pressure in mm mercury is P = H-h, where H is the barometer height.
• The tap is opened and the pressure above water varied using the pump to a suitable value.
• The tap is closed and water in the flask in heated until it boil.
• The temperature θ and difference in mercury levels, h, are noted and recorded.
• The saturated vapour pressure, P = (His calculated
• The procedure is repeated other values of θ and h
• A graph of P versus θ is plotted and the saturated vapour pressure at a particular temperature is obtained.

Example 33

With the aid of a labelled diagram, describe an experiment to determine standard saturated vapour pressure of water. (05marks)

Example 34

Use the kinetic theory to explain the following observations

(i) Saturated vapour pressure of a liquid increases with temperature. (03marks)

If a liquid is in dynamic equilibrium with its vapour, an increase in temperature increases mean kinetic energy of the molecules and hence the rate at which molecules escape from the liquid.

The density of the vapour increases implying increase in the rate of condensation until dynamic equilibrium is restored. There are now more molecules in the vapour phase than previously that are moving faster and hence higher pressure.

(ii) Saturated vapour pressure is not affected by decrease in volume at constant pressure. (03marks)

A decrease in volume leads to a momentary increase in vapour density. Consequently, the rate of condensation increases while the rate of evaporation rate is constant. When the vapour density reduces, the condensation rate also reduces. So the dynamic equilibrium is restored to the initial value.

Example 35

Two similar cylinders P and Q contain different gases at the same pressure. When gas is released from P the pressure remains constant for some time before it starts dropping. When gas is released from Q the pressure continuously drops. Explain the observation above. (05marks)

• The gas in P is in form of a saturated vapour; that is, in dynamic equilibrium with a liquid. As the gas is released, more liquid turns into a gas to restore pressure until the gas becomes unsaturated and the pressure begins to drop as the moles of the gas decrease
• The gas in Q is unsaturated, and thus pressure reduces as the moles of the gas reduces up on release.

Experiment to show that a liquid boils off when its saturated vapour pressure equals the external pressure

• Air is trapped in the closed limb of the tube by water column.
• The tube is heated in water bath.
• When the water bath begins to boil, the water in the tube comes to the same level in each limb.
• This shows that the vapor pressure in closed limb is equal to external pressure.

 

Evaporation

During evaporation, a liquid changes to vapour low the boiling point.

Reasons why evaporation causes cooling

During evaporation liquid molecules with high kinetic energy escape from inter molecular attraction in the liquid leaving molecules of low kinetic energy behind.  Since temperature s proportional average kinetic energy of molecules, the liquid cools.

Factors affecting the rate of evaporation

• Surface area. Evaporation increases with surface area of a liquid due to increase in the number of exposed molecules.
• Temperature: increase in temperature increases the rate of evaporation because it increases the average kinetic energy of the molecules.
• Drought /wind blowing over the surface. Wind removes the saturated air layer from the surface of the liquid thereby increasing the rate of evaporation.

Example 36

Explain the occurrence   of land and sea breeze. (04marks)

During day, the land is heated to a high temperature than the sea. Hot air expands and rises from land. A stream of cool air from the sea blows towards the land to replace the uprising air, hence sea breeze occurs.

At night the land cools faster because it is no longer heated by the sun. The sea retains the warmth because it is heated deeply. Warm less dense air rises from the sea surface and air from land blows to replace it leading to land breeze.

Example 37

A horizontal tube of uniform bore, closed at one end, has some air trapped by a small quantity of water. The length of the enclosed air column is 20cm at 12⁰C.

Find stating any assumptions made, the length of air column when the temperature is raised to 38⁰C.

[S.V.P of water at 12⁰C and 38⁰C are 10.5mmHg and 49.5mmHg respectively. Atmospheric pressure = 75cmHG] (05marks)

Assumption: the tube does not expand when the temperature increases.

 Example 38

When hydrogen gas is collected over water, the pressure in the tube at 15⁰C and 75⁰C are 65.5cm and 105.6cm of mercury respectively. If the saturated vapour pressure at 15⁰C is 1.42cm of mercury, find its value at 75⁰C (04marks)

P₁= 65.5 – 1.42 = 62.08 and T₁ = 273 + 15 = 288K

P₂ = 105.6 – P, and T₂ = 273 + 75 = 348K

 

Isothermal and adiabatic changes

Isothermal expansion takes place at constant temperature.

Adiabatic expansion takes place at constant heat.

Sketch graphs of pressure versus volume for fixed mass of a gas undergoing isothermal and adiabatic changes.

Condition necessary for realization of an isothermal change

• The gas must be held in thin-walled and highly conducting vessel
• The process must take place slowly so that heat pass into the gas to maintain constant temperature.
• The gas vessel must be surrounded by a constant temperature bath.

Conditions for adiabatic change

• The gas must be held in a thick walled and poorly conducting vessel
• The process must be carried out rapidly to minimize heat linkage through the walls.

 

Relationship between volume, pressure and temperature

(i) For reversible isothermal change

PV = nRT where n is the number of mole of  gas, R = gas constant

(ii) For reversible adiabatic change

Pv^γ = constant

TV^γ-1 = constant

Example 39

Ten moles of a gas, initially at 27⁰C are heated at constant pressure of 1.01 x 10⁵Pa and volume increased from 0.25m³ to 0.375m³. Calculate the increase in internal energy.

[Assume C_p = 28.5Jmol^-1K^-1] (06marks)

Example 40

An ideal gas at 18⁰C is compressed adiabatically until the volume is halved. Calculate the final temperature of the gas. [Assume specific heat capacities of the gas at constant pressure and volume are 2100Jkg^-1K^-1 and 1500Jkg^-1K^-1] respectively. (04marks)

Example 41

State the first law of thermodynamics and use it to distinguish between Isothermal and adiabatic changes in a gas. (05marks)

ΔQ = ΔU + ΔW = nC_vΔT + ΔW

During isothermal expansion, ΔT = 0. Therefore all the energy supplied is equal to the work done by the gas during expansion.

In adiabatic expansion, no heat enters or leaves the gas. Therefore ΔQ = 0 and ΔU = -ΔW.

In adiabatic expansion, work s done at the expense of its internal energy. Therefore the gas cools.

Example 42

(a) (i) What is meant by isothermal process and adiabatic process. (02marks)

Isothermal process is the expansion or compression of a gas at constant temperature.

Adiabatic process is the expansion or compression of a gas where there is no heat loss or gain into the gas.

(ii) Explain why adiabatic expansion of a gas causes cooling (03marks)

During an adiabatic expansion of a gas, no heat is supplied to the gas. Molecules strike the receding piston and bounce off with reduced velocities and hence lower kinetic energy. Since kinetic energy is proportional to temperature, the gas cools during the expansion

 

(b) A gas at a temperature of 17⁰C and pressure 1.0 x 10⁵Pa compressed isothermally to half its original volume. It is then allowed to expand adiabatically to its original volume

(i) Sketch a P-V curve the above process (02marks)

(ii) If the specific heat capacity at constant pressure is 2100Jmol^-1K^-1 and at constant volume is 1500Jmol^-1K^-1, find the final temperature of the gas (04marks)

 

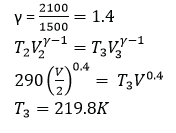
Heat transfer

Conduction

Conduction is the transfer of heat from a region of high temperature to that of low temperature without a resultant movement of the molecules of conducting material.

Mechanisms of heat conduction

(a) Metals

• The atoms of metals consist of free mobile electrons; when one end of a metal is heated, these free electrons travel at high speed and collide with other electrons and atoms. In this way heat is transferred quickly from a hot end to a cold end.
• Secondly when one end of a metal is heated atoms vibrate with high frequency and amplitude; collide with other atoms to which they give heat. Those atoms that receive heat also vibrate with high frequency and amplitude, collide and transfer their heat. In this way heat energy is transferred from one part of the metal to another.

(b) Non-metals

• In non-metal heat is transferred by interatomic vibrations.
• When one end of a metal is heated atoms vibrate with high frequency and amplitude; collide with other atoms to which they give heat. Those atoms that receive heat also vibrate with high frequency and amplitude, collide and transfer their heat. In this way heat energy is transferred from one part of the metal to another

(c) Heat transfer in gases

Heat energy in gases is transferred by molecular collisions between hot and cold molecules. When a gas is heated, the fast moving molecules collide and pass on their kinetic energy to cold slower molecules.

Temperature distribution along a conductor

(i) lagged  metal

The rate of heat flow along the bar is constant since heat loss is negligible.

(ii) Unlagged or exposed to the surrounding

The rate of heat flow decrease with length due to heat losses

Example 43

The two ends of a metal bar of length 1.0m are perfectly lagged up to 20cm from either end. The ends of the bar maintained at 100⁰C and 0⁰C respectively.

(i) Sketch a graph of temperature versus distance of a bar. (02marks)

(ii)Explain the features of the graph in (b)(i)(03marks)

• In lagged portions there is constant heat flow because there I no heat loss to the surroundings
• In unlagged portion heat flow is not uniform due to heat loss to the environment.

 

Thermal conductivity.

Thermal conductivity is the rate of heat transfer per unit cross section area per unit temperature gradient

Factors affecting the rate of heat flow

• Temperature gradient
• Cross-section area

 Measurement of thermal conductivity of a good conductor (e.g. metal)

Conditions

• Heat must flow through the specimen at measurable rate
• The temperature gradient along the specimen must be measurably steep. i.e. the specimen bar must be longer than it diameter.

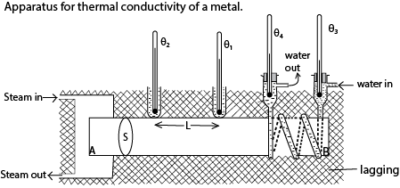
• Specimen bar AB of mean diameter, d, is heated by steam at end A and cooled by water at end B as shown above
• The lagging ensure a constant rate of heat flow
• The setup is left to run for some time until steady temperatures θ₁, θ₂, θ₃ and θ₄ are obtained.
• The rate water flow m kgs^-1 is measured using a cylinder and stop clock.

where k = thermal conductivity of the metal and c_w is specific heat  capacity of water

 

Measurement of thermal conductivity of a bad conductor (e.g. glass, cork)

• Glass s cut in form of a thin disc of cross section area, A and thickness, x.
• The disc is sandwiched between a steam chest and brass slab of mass, m and specific heat capacity, c.
• Steam is passed through the chest until the thermometers register steady temperatures, θ₁ and θ₂.

• The glass disc is removed and brass slab is heated directly by steam chest, until its temperature is about 10⁰C above θ₁.
• Steam chest is removes and the top of the glass slab is covered by the glass disc.
• The temperature of the slab is recorded at suitable time interval until its temperature is about 10⁰C below θ₁.
• A graph of temperature against time is plotted and its slope s determined at θ₁

Precautions

• Sample in a thin disc
• Faces of the disc highly polished to ensure tight uniform contacts
• A thin layer of grease is smeared on faces for good thermal contact.

 

Example 44

A cylindrical iron vessel with a base of diameter 15cm and thickness 0.30cm has its base coated with a thin film of soot of thickness 0.10cm. It is then filled with water at 100⁰C and placed on a large block of ice at 0⁰C. Calculate the initial rate at which the ice will melt (06marks) (thermal conductivity of soot=0.12Wm^-1K^-1, Thermal conductivity of iron, k = 75Wm^-1K^-1)

Example 45

A window of height 1.0m and width 1.5m contains a double grazed unit consisting of two single glass panes, each of thickness 4.0mm separated by an air gap of 2.0mm. Calculate the rate at which heat is conducted through the window if the temperatures of external surfaces of glass are 20⁰C and 30⁰Crespectively.

[Thermal conductivities of glass and air are 0.72Wm^-1K^-1 and 0.025 Wm^-1K^-1 respectively] (07marks)

Example 46

Explain why heating system based on the circulation of steam are more efficient than those based on circulation of boiling water. (02marks)

A given mass of steam gives out more energy that an equal amount of water because of the specific latent heat

Radiation

Thermal radiation is the transfer of heat through vacuum i.e. no material medium is required for this transmission.

A black body radiation is an electromagnetic radiation emitted by a body solely due its temperature i.e. energy emitted depends on body’s temperature.

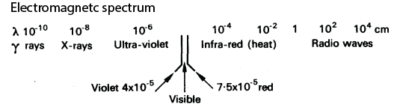
Electromagnetic spectrum

Electromagnetic spectrum is the distribution of electoral magnetic radiations ranging from those of short wave length to those of longer wave length as shown below.

Infrared radiations

Infrared radiations are electromagnetic radiations which are converted into heat when they strike a surface.

Properties of infrared radiations.

• They travel at the speed of light.
• They are reflected and refracted like light.
• When absorbed by a body the body’s temperature is raised.
• Causes photo-electric emission from surfaces like Cesium.
• Affects special types of photographic plates which enable pictures to be taken in the dark.
• They are absorbed by glass but transmitted by rock salt and quartz.

Comparison of radiation ability for different surfaces

A cubical metal tank whose sides are painted; dull black, dull white and highly polished is filled with hot water and radiations from each surface are detected by a thermopile as shown below.

The galvanometer deflection is greatest when the thermopile is facing the dull black surface and least when facing a highly polished silver surface. Therefore, a polished surface is the least radiator and a black surface is the best radiator.

 

Detectors of infrared radiation

(a) Barometer

The bolometer strip is connected to Wheatstone bridge circuit above. The rheostat is adjusted until the galvanometer shows no deflection. When the radiations fall on the strip, they are absorbed and its temperature rises leading to an increase in resistance. The galvanometer deflects showing the presence of radiations.

 

(b) a thermopile

Radiation falling on junction A is absorbed and temperature rises above that of junction B. An e.m.f is generated and is measured by millivolt meter which deflects as a result.

 

(c) The ether-thermo scope.

A blackened and clear bulbs are connected to a tube partly filled with ether i.e. each bulb contains mixture of air and ether vapour. When the arrangement is exposed to infrared radiations, more radiations are absorbed by the blackened bulb than those absorbed by the clear bulb. This raises the pressure inside the blackened bulb causing the ether liquid to be raised in the unblackened bulb as shown below.

The rise h is proportional to incident radiation

Black body

• A black body is one which absorbs all radiations incident on it and reflects or transmits none.
• The radiations emitted by a black body are called temperature radiations or black body radiations.

Approximation of black body

When radiation enters a black container through a hole, it undergoes multiple reflections. At each reflection, part of the radiation is absorbed. After several reflections, all the radiation is retained inside the container. Hence it approximates to a black body.

Distribution of black body radiation

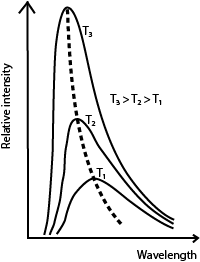
• For every wave length, relative intensity increases as temperature is increased.
• The wavelength at which maximum intensity occur shifts to the shorter wavelength as temperature is increased.
• l _max is the wavelength of radiation emitted at maximum intensity/emission of a black body at a particular temperature.

Laws of black body radiation

(a) Wien’s displacement law

If λ_max is the wavelength of the peak of the curve for a given temperature, T then

λ_maxT = constant; the constant is Wien’s constant = 2.9 x 10^-3mK

(b) If E λ_max is the height of the peak of the curve for temperature, T, then,

(c) The curve showing the variation of E_λ with λat a constant temperature obeys the Plank formula;         where c₁and c₂ are constant

(d) State Stefan’s law.

Stefan’s law states that the total power radiated by a black body per unit surface area is proportional to the fourth power of its absolute temperature. i.e.,

If E is the total energy radiated per second per m² area of a black body at temperature T, then E = σT^4; where σ is called Stefan’s constant = 5.67 x 10^-8Wm^-2K^-4.

Example 47

The earth receives energy from the earth from the sun at the rate of 1.4 x 10³Wm^-2. If the ratio of the earth’s orbit to the sun’s radius is 216, calculate the surface temperature of the sum. (05marks)

Power radiated by the sun = 4πr²σT⁴

Example 48

A spherical black body of radius 2.0cm at -73⁰C is suspended in an evacuated enclosure whose walls are maintained at 27⁰C. If the rate of exchange of thermal energy is equal to 1.85Js^-1,

(i) find the value of Stefan’s constant, (05marks)

(ii) (Calculate the wavelength at which the radiation emitted by the enclosure ha maximum intensity (03mark)

Prevost’s theory of heat exchange

When a body is in thermal equilibrium with its surrounding, its rate of emission of radiation to surrounding is equal to the rate of absorption of the radiation from the surrounding.

Example 49

A small blackened solid copper sphere of radius 2cm is placed in an evacuated enclosure whose wall are kept at 100⁰C. Find the rate at which energy must be supplied to the sphere to keep its temperature at 127⁰C. (03marks)

Example 50

The energy intensity received by a spherical planet from a star is 1.4 x 10³Wm^-2. The star is of radius 7.0 x 10⁵km and is 14.0 x 10⁷km from the planet.

(i) Calculate the surface temperature of the star. (04marks)

(ii) State any assumptions you have made in (c)(i) above (01marks)

• The star is spherical
• thestar radiates as a black body
• There is no heat loss to the sphere

 

Greenhouse effect and global warming

• When short wavelength infrared radiation from the sun pass through the water vapour and carbon dioxide in lower layers of the atmosphere, the radiation is absorbed by the earth warming it up.
• The earth re-emits this radiation (infrared) as black body radiation of long wavelength (because of low temperature) and therefore it is trapped by the water vapour and carbon dioxide in the earth’s atmosphere.
• Since the radiation is prevented from escaping from the earth’s atmosphere, it causes global warming.

Please download PDF: Heat notes (A-level)

Thank you

Compiled by Dr. Bbosa Science

Sponsored by the Science Foundation College

+ 256 753 802709